浙江省台州市仙居县两校联考2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-10-21 类型：期中考试

进入出卷网下载

一、单选题

1. 在2020，1，0，﹣2021中，最小的数是（）

A、2020 B、1 C、0 D、﹣2021

查看试题解析
2. 计算（﹣3）²的结果为（）

A、9 B、6 C、﹣9 D、﹣6

查看试题解析
3. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作，根据规划“一带一路”地区覆盖总人口为4400000000人.4400000000这个数用科学记数法表示为（）

A、 $44 \times 1 0^{8}$ B、 $4.4 \times 1 0^{8}$ C、 $4.4 \times 1 0^{9}$ D、 $4.4 \times 1 0^{10}$

查看试题解析
4. 方程 $2 x - 4 = 0$ 的解是（）

A、 $x = - 2$ B、 $x = 0$ C、 $x = 2$ D、 $x = \frac{1}{2}$

查看试题解析
5. 多项式 $- x^{2} - \frac{1}{2} x - 1$ 的各项分别是（）

A、 $- x^{2}, \frac{1}{2} x, 1$ B、 $- x^{2}, - \frac{1}{2} x, - 1$ C、 $x^{2}, \frac{1}{2} x, 1$ D、 $x^{2}, - \frac{1}{2} x, - 1$

查看试题解析
6. 已知a＝b，下列四个式子中，不正确的是（）

A、2a＝2b B、﹣2a＝﹣2b C、a+2＝b﹣2 D、a﹣2＝b﹣2

查看试题解析
7. ﹣（a﹣b+c）变形后的结果是（）

A、﹣a+b+c B、﹣a+b﹣c C、﹣a﹣b+c D、﹣a﹣b﹣c

查看试题解析
8. 若x＝4是方程 $\frac{x}{2} - a$ ＝4的解，则a等于（）

A、0 B、 $\frac{1}{2}$ C、﹣3 D、﹣2

查看试题解析
9. 如图，两个三角形的面积分别是 7 和 3，对应阴影部分的面积分别是 m、n，则 m﹣n 等于（）

A、4 B、3 C、2 D、不能确定

查看试题解析
10. 如图所示，圆的周长为4个单位长度，在圆周的4等分点处标上字母A，B，C，D，先将圆周上的字母A对应的点与数轴的数字1所对应的点重合，若将圆沿着数轴向左滚动、那么数轴上的﹣2019所对应的点与圆周上字母（）所对应的点重合．

A、A B、B C、C D、D

查看试题解析

二、填空题

11. $- \sqrt{2}$ 的绝对值是.

查看试题解析
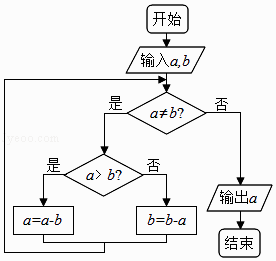
12. 计算：3a－2a＝.

查看试题解析
13. 已知铅笔每支m元，橡皮每块n元，若买两支铅笔和三块橡皮，则一共需付款元．

查看试题解析
14. 把一批图书分给同学，若每人分3本，则剩下20本，若每人分4本，则还差25本．问有多少同学？若设有x名同学，则可列方程．

查看试题解析
15. 如图，程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行程序框图，如果输入a，b的值分别为3，9，那么输出a的值为．

查看试题解析
16. 如图，将正整数按此规律排列成数表，则2021是表中第行第列.

查看试题解析

三、解答题

17. 计算：

(1)、（﹣5）+9；

(2)、3﹣（﹣2）；

(3)、5×（﹣6）．

查看试题解析
18. 计算：

(1)、2²×（﹣3）﹣（﹣2）³÷4；

(2)、﹣42×（ $\frac{2}{3}$ ﹣ $\frac{2}{7}$ + $\frac{1}{6}$ ﹣ $\frac{3}{14}$ ）．

查看试题解析
19. 在数轴上画出表示0，﹣0.5，﹣3， $\frac{1}{2}$ ， $\frac{7}{2}$ 的点，并把它们按从小到大的顺序用“＜”连接起来．

查看试题解析
20. 化简下列各式

(1)、﹣ab+7ab﹣9ab；

(2)、（3x²﹣xy﹣2y²）﹣2（x²+xy﹣2y²）．

查看试题解析
21. 先化简，再求值：2（x²y+3xy）﹣3（x²y﹣1）﹣2xy﹣2，其中x＝﹣2，y＝2．

查看试题解析
22. 解方程：

(1)、3x＝x﹣2；

(2)、8﹣x＝3x+2．

查看试题解析
23. 为了加强公民的节水意识，合理利用水资源，某市采用价格调控手段以达到节水的目的. 该市自来水收费价格见价目表.

(1)、填空：若该户居民2月份用水4m³ ，则应收水费元；

(2)、若该户居民3月份用水am³（其中6<a<10），则应收水费多少元？（用a的整式表示并化简）

(3)、若该户居民4，5月份共用水15m³（5月份用水量超过了4月份），设4月份用水xm³ ，求该户居民4，5月份共交水费多少元？（用x的整式表示并化简）

查看试题解析
24. 在数轴上，把表示数1的点称为基准点，记作点 $∮$ ．对于两个不同的点M和N，若点M、点N到点 $∮$ 的距离相等，则称点M与点N互为基准变换点．例如：图1中，点M表示数-1，点N表示数3，它们与基准点 $∮$ 的距离都是2个单位长度，点M与点N互为基准变换点．

(1)、已知点A表示数a，点B表示数b，点A与点B互为基准变换点．
①若a=0，则b=；若a=4，则b=；
②用含a的式子表示b，则b=；

(2)、对点A进行如下操作：先把点A表示的数乘以2.5，再把所得数表示的点沿着数轴向左移动3个单位长度得到点B．若点A与点B互为基准变换点，则点A表示的数是；

(3)、点P在点Q的左边，点P与点Q之间的距离为8个单位长度．对P、Q两点做如下操作：点P沿数轴向右移动k（k>0）个单位长度得到 $P_{1}$ ， $P_{2}$ 为 $P_{1}$ 的基准变换点，点 $P_{2}$ 沿数轴向右移动k个单位长度得到 $P_{3}$ ， $P_{4}$ 为 $P_{3}$ 的基准变换点，…，依此顺序不断地重复，得到 $P_{5}$ ， $P_{6}$ ， …， $P_{n}$ ． $Q_{1}$ 为Q的基准变换点，将数轴沿原点对折后 $Q_{1}$ 的落点为 $Q_{2}$ ， $Q_{3}$ 为 $Q_{2}$ 的基准变换点，将数轴沿原点对折后 $Q_{3}$ 的落点为 $Q_{4}$ ， …，依此顺序不断地重复，得到 $Q_{5}$ ， $Q_{6}$ ， …， $Q_{n}$ ．若无论k为何值， $P_{n}$ 与 $Q_{n}$ 两点间的距离都是4，则n=

查看试题解析