四川省成都市东部新区2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-10-21 类型：期中考试

进入出卷网下载

一、单选题

1. 在﹣|6|，﹣20%，﹣（﹣5），0，（﹣1）² ， +7³中，负数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 共享单车为市民短距离出行带来了极大便利．据2017年“深圳互联网自行车发展评估报告”披露，深圳市日均使用共享单车2590000人次，其中2590000用科学记数法表示为（）

A、259×10⁴ B、25.9×10⁵ C、2.59×10⁶ D、0.259×10⁷

查看试题解析
3. 代数式 $\frac{a}{3}$ ， 0， $\frac{1}{x}$ ， 2ab+6， $\frac{3 x^{2}}{π}$ ， ﹣m中，整式共有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
4. 下列图形是正方体的表面展开图的是（）

A、 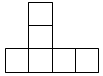B、 C、 D、

查看试题解析
5. 如果单项式2anb²c是六次单项式，那么n的值取（）

A、6 B、5 C、4 D、3

查看试题解析
6. 下列图形绕虚线旋转一周，能形成圆柱体的是（）

A、 B、 C、 D、

查看试题解析
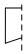7. 下列计算正确的是（）

A、6b﹣5b＝1 B、2m+3m²＝5m³ C、﹣（a﹣b）＝﹣a﹣b D、﹣2（c﹣d）＝﹣2c+2d

查看试题解析
8. 点A在数轴上距原点3个单位长度，若一个点从点A处左移4个单位长度，此时终点所表示的数是（）

A、﹣1 B、±1 C、±7 D、﹣1或﹣7

查看试题解析
9. 若a、b互为相反数，c为最大的负整数，d的倒数等于它本身，则2a+2b-cd的值是（）

A、1 B、-2 C、-1 D、1或-1

查看试题解析
10. 按如图所示的运算程序，能使运算输出结果为 $- 5$ 的是（）

A、 $x = 1$ ， $y = - 2$ B、 $x = 1$ ， $y = 2$ C、 $x = - 1$ ， $y = 2$ D、 $x = - 1$ ， $y = - 2$

查看试题解析

二、填空题

11. 在①长方体、②球、③圆锥、④圆柱、⑤正方体、⑥三棱柱这六种几何体中，其主视图、左视图、俯视图都完全相同的是（填上序号即可）．

查看试题解析
12. 比较大小： $- \frac{7}{8}$ $- \frac{8}{9}$ .

查看试题解析
13. 若x﹣3y＝5，则代数式2x﹣6y+2011的值为．

查看试题解析
14. 某件商品的成本价为a元，按成本价提高30%后标价，再以8折（即按标价的80%）销售，这件商品的售价为元．

查看试题解析
15. 当x＝﹣1时，代数式ax²+2bx+1的值为0，则﹣2a+4b﹣3＝．

查看试题解析
16. 在数轴上表示a、b两个实数的点的位置如图所示，则化简 $| a - b |$ － $| a + b |$ 的结果是．

查看试题解析
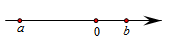17. 用若干个大小相同的小立方块搭一个几何体，使得从正面和从上面看到的这个几何体的形状如图所示，则搭出这个几何体至少需要个小立方体，最多需要个小立方体.

查看试题解析
18. 三个有理a、b、c满足abc＜0，（a+b）（b+c）（a+c）＝0，则代数式 $\frac{| a |}{3 a} + \frac{| b |}{3 b} + \frac{| c |}{3 c}$ 的值为．

查看试题解析
19. 已知整数a₁ ， a₂ ， a₃ ， a₄ ， …，an满足下列条件：a₁＝0，a₂＝|a₁﹣1|，a₃＝|a₂﹣2|，a₄＝|a₃﹣3|，…，an＝|an_﹣₁﹣（n﹣1）|，以此类推，则a₂₀₂₁的值为．

查看试题解析

三、解答题

20. 计算：

(1)、 $- 32 - (- 14) + 4$ ；

(2)、 $\frac{8}{15} \div (\frac{1}{3} - 1) \times 2 \frac{1}{2}$

(3)、 $37 - (\frac{7}{9} - \frac{1}{6}) \times {(- 6)}^{2}$

(4)、 $- 2^{2} \div (- 3) - \frac{1}{3} \times [4 - {(- 6)}^{2}]$

查看试题解析
21. 计算或化简求值：

(1)、5m﹣2（4m+5n）+3（3m﹣4n）．

(2)、先化简，再求值：5（3a²b﹣ab²）﹣（ab²+3a²b），其中 $a = - \frac{1}{2}$ ， $b = \frac{1}{3}$ ．

查看试题解析
22. 如图所示是一个用小立方体搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方体的个数，请你画出它的主视图与左视图．

查看试题解析
23. 将图1中的正方形剪开得到图2，则图2中共有4个正方形；将图2中的一个正方形剪开得到图3；将图3中4个较小的正方形中的一个剪开得到图4，…，照这个规律剪下去：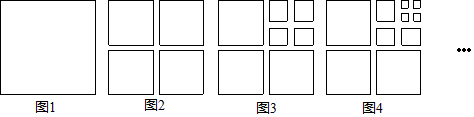

(1)、根据图中的规律补全表．
图形标号
1
2
3
4
…
正方形个数
1
4
…

(2)、第n个图中有多少个正方形？

(3)、第2021个图中有多少个正方形？

查看试题解析
24. 为了提高足球球员快速抢断转身能力，教练设计了折返跑训练．在足球场上画一条东西方向的直线，如果约定向东为正，向西为负，一组折返跑训练的记录如下（单位：米）：40，﹣30，+50，﹣25，+25，﹣30，+15，﹣28，+16，﹣18．

(1)、球员最后到达的地方在出发点的哪个方向？距出发点多远？

(2)、在这组训练过程中，球员最远处离出发点多远？

(3)、球员在这组训练过程中，共跑了多少米？

查看试题解析
25. 我区居民生活用水实行阶梯式计量水价，据了解，实行的阶梯式计量水价分为三级（如表所示）：

月用水量
水价（元/吨）
第1级
20吨以下（含20吨）
1.65
第2级
20吨～30吨（含30吨）
2.48
第3级
30吨以上
3.30
例：李老师家2019年7月份的用水量为35吨，按三级计算则应缴水费为：
20×1.65+10×2.48+（35﹣20﹣10）×3.30＝74.3（元）．

(1)、如果鲜老师家2019年8月份的用水量为10吨，则需缴水费元；

(2)、如果叶老师家2019年9月份的用水量为a吨，叶老师家该月应缴水费多少元？（用含a的代数式表示，并化简；

(3)、如果钟老师家2019年10月份应缴水费54.08元，则钟老师家该月用水量为多少吨？

查看试题解析
26. 已知A＝a﹣2ab+b² ， B＝a+2ab+b².

(1)、求 $\frac{1}{4}$ （B﹣A）的值；

(2)、若3A﹣2B的值与a的取值无关，求b的值.

查看试题解析
27. 如图，是由一些棱长为a厘米的正方体小木块搭建成的几何体的从正面看、从左面看和从上面看的图形．

(1)、该几何体是由多少块小木块组成的？

(2)、求出该几何体的体积；

(3)、求出该几何体的表面积（包含底面）．

查看试题解析
28. 如图A在数轴上所对应的数为﹣2．

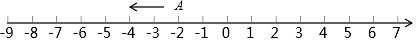(1)、点B在点A右边距A点4个单位长度，求点B所对应的数；

(2)、在（1）的条件下，点A以每秒2个单位长度沿数轴向左运动，点B以每秒2个单位长度沿数轴向右运动，当点A运动到﹣6所在的点处时，求A，B两点间距离．

(3)、在（2）的条件下，现A点静止不动，B点沿数轴向左运动时，经过多长时间A，B两点相距4个单位长度．

查看试题解析

	月用水量	水价（元/吨）
第1级	20吨以下（含20吨）	1.65
第2级	20吨～30吨（含30吨）	2.48
第3级	30吨以上	3.30

图形标号	1	2	3	4	…
正方形个数	1	4			…