广东省云浮市罗定市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-10-21 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $y = \sqrt{x - 5} + \sqrt{5 - x} - 3$ ，则 $x y =$ （）

A、－15 B、－9 C、9 D、15

查看试题解析
2. 斜边长是4的直角三角形，它的两条直角边可能是（）

A、3， $\sqrt{7}$ B、2，3 C、3，5 D、2，2

查看试题解析
3. 如图，▱ABCD中，点O是对角线AC的中点，点E是BC的中点，CD＝8，则OE＝（）

A、3 B、4 C、5 D、7

查看试题解析
4. 某班共有35位同学参加了学校组织的数学解题大赛，下表为该班参赛成绩的频数分布表，该班数学成绩的众数为（）
成绩（分）
20
30
40
50
60
70
90
100
频数（人）
1
3
3
9
8
4
3
4

A、60分 B、50分 C、3人 D、9人

查看试题解析
5. 汽车由 $A$ 地驶往相距 $120 k m$ 的 $B$ 地，它的平均速度是 $30 k m / h$ ，则汽车距 $B$ 地路程 $s (k m)$ 与行驶时间 $t (h)$ 的关系式为（）

A、 $s = 120 - 30 t$ B、 $s = 120 + 30 t$ C、 $s = 30 t$ D、 $s = 120 t$

查看试题解析
6. 如图，点E，F，G，H分别为四边形ABCD的边AB，BC，CD，DA的中点．下列三种说法：
① .四边形EFGH一定是平行四边形；
②.若AC＝BD，则四边形EFGH 是菱形；
③.若AC⊥BD，则四边形EFGH是矩形．
其中正确的是（）

A、① B、①② C、①③ D、①②③

查看试题解析
7. 估计 $\sqrt{2} \div \sqrt{\frac{1}{10}} + \sqrt{5}$ 的值应在（）

A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间

查看试题解析
8. 如图，平行四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O，点E是 $A D$ 中点．若 $O A = 2 ， △ A O E$ 的周长为10，则平行四边形 $A B C D$ 的周长为（）

A、16 B、32 C、36 D、40

查看试题解析
9. 甲乙两车均从 $A$ 地开往相距 $300 k m$ 的 $B$ 地，如图，反映了甲乙两车的路程 $y$ （单位： $k m$ ）之间的关系，下列结论正确的是（）

A、甲车的速度为 $75 k m / h$ B、甲乙两车同时从 $A$ 地出发 C、乙车比甲车提前1小时到 $B$ 地 D、甲车行驶1.5小时追上乙车

查看试题解析
10. 对于实数 $a ， b$ ，定义符号 $m i n {a ， b}$ 其意义为：当 $a \geq b$ 时， $m i n {a ， b} = b$ ；当 $a < b$ 时， $m i n {a ， b} = a$ ．例如： $m i n {2 ， - 1} = - 1$ ，若关于 $x$ 的函数 $y = m i n {2 x - 1 ， - x + 3}$ ，则该函数的最大值是（）

A、1 B、 $\frac{4}{3}$ C、 $\frac{5}{3}$ D、2

查看试题解析

二、填空题

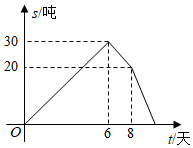
11. 正比例函数y＝kx （k是常数，k≠0）的图象是一条经过的直线，我们称它为直线y＝kx．

查看试题解析
12. 甲、乙两名同学参加“古诗词大赛”活动，五次比赛成绩的平均分都是85分，如果甲比赛成绩的方差为 $S_{甲}^{2}$ ＝16.7，乙比赛成绩的方差为 $S_{乙}^{2}$ ＝28.3，那么成绩比较稳定的是(填“甲”或“乙”)．

查看试题解析
13. 已知平行四边形的周长是24，相邻两条边的长度相差4，那么较短边长为．

查看试题解析
14. 直线 $y = k x + b$ 经过 $A (- 20 ， 5)$ 、 $B (10 ， 20)$ 两点，求这条直线与两坐标轴围成的三角形的面积是．

查看试题解析
15. 春耕期间，市农资公司连续8天调进一批化肥，并在开始调进化肥的第七天开始销售．若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变，这个公司的化肥存量s（单位：吨）与时间t（单位：天）之间的函数关系如图所示，则该公司这次化肥销售活动（从开始进货到销售完毕）所用的时间是天．

查看试题解析
16. 如图，直线 $l$ 与 $x$ 轴交于点 $A (6 ， 0)$ ，与 $y$ 轴交点 $B (0 ， 3)$ ，点 $M (a ， 2)$ 是直线 $l$ 上一点，过点 $M$ 的直线 $M N$ 交边 $O A$ 点 $N$ ，若直线 $M N$ 将 $△ A O B$ 分成面积相等的两部分，则点 $N$ 的坐标是．

查看试题解析
17. 如图，在菱形 $A B C D$ 中， $A B = 8$ ， $E$ 是 $B C$ 边的中点， $P$ 是菱形 $A B C D$ 内一动点，若 $△ P B E$ 的面积是6，则 $P B + P E$ 的最小值是．

查看试题解析

三、解答题

18. 先化简，再求值： $(\frac{x + 3}{x^{2} - 1} - \frac{2}{x - 1}) \div \frac{x + 2}{x^{2} + x}$ ，其中 $x = \sqrt{2} - 2$ ．

查看试题解析
19. 为了解本校八年级学生的音乐知识掌握情况，本老师随机抽取35名学生进行了一次音乐知识测试，根据测试成绩制成统计图表．
组别
分数段
人数
A
$x < 60$
2
B
$60 \leq x < 75$
5
C
$75 \leq x < 90$
a
D
$x \geq 90$
12
请根据上述信息解答下列问题：

(1)、本次调查属于调查，样本容量是；

(2)、表中的 $a =$ ，样本数据的中位数位于组；

(3)、补全条形统计图：

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $∠ A B C$ 和 $∠ B C D$ 的角平分线 $B E$ 与 $C E$ 相交于点 $E$ ，且点 $E$ 恰好落在 $A D$ 上；

(1)、求证： $B E^{2} + C E^{2} = B C^{2}$

(2)、若 $A B = 2$ ，求 $▱ A B C D$ 的周长．

查看试题解析
21. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．
小明在练习操控航拍无人机，该型号无人机在上升和下降的速度相同，设无人机的飞行高度 $y m$ ，小明操控无人机的时间 $x m i n$ ，给出的图象反映了这个过程中 $y m$ 与 $x m i n$ 之间的对应关系．
请根据相关信息，解答下列问题：

(1)、填表：
无人机飞行的时间/ $m i n$
0.5
1.5
3
5
7
无人机飞行的高度/ $m$
10
40

(2)、填空：
①无人机上升的速度为 $m / m i n$ ；
②无人机在第分钟开始下降的；

(3)、当 $5 \leq x \leq 12$ 时，请直接写出 $y$ 关于 $x$ 的函数解析式；

(4)、当无人机距高地面的高度为 $50 m$ 时，直接写出 $x$ 的值．

查看试题解析
22. 如图， $B D$ 、 $A C$ 是四边形 $A B C D$ 的对角线，点E、F、G、H分别是线段 $A D$ 、 $D B$ 、 $B C$ 、 $A C$ 上的中点

(1)、求证：线段 $E G$ 、 $F H$ 互相平分；

(2)、四边形 $A B C D$ 满足什么条件时， $E G ⊥ F H$ ？证明你得到的结论．

查看试题解析
23. 如图， $A D$ 是 $△ A B C$ 的角平分线， $D E ⊥ A B$ ， $D F ⊥ A C$ ，垂足分别是E、F，连接 $E F$ ， $E F$ 与 $A D$ 相交千点H．

(1)、求证： $A D ⊥ E F$ ；

(2)、 $△ A B C$ 满足什么条件时，四边形 $A E D F$ 是正方形？说明理由．

查看试题解析
24. 如图，直线y＝－2x与直线y＝kx＋b相交于点A(a，2)，并且直线y＝kx＋b经过x轴上点B(2，0)．

(1)、求直线y＝kx＋b的解析式；

(2)、求两条直线与y轴围成的三角形面积；

(3)、直接写出不等式(k＋2)x＋b≥0的解集．

查看试题解析
25.

(1)、如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段AE与MN之间的数量关系，并说明理由．

(2)、如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，CQ（图中未连），判断线段EQ与CQ之间的数量关系，并说明理由．

(3)、在（2）的条件下延长EQ交边AD于点F．则∠AEF=°；

(4)、如图3，若该正方形ABCD边长为8，将正方形沿着直线MN翻折，使得BC的对应边B′C′恰好经过点A，过点A作AG⊥MN，垂足分别为G，若AG＝5，请直接写出AC′的长．

查看试题解析

组别	分数段	人数
A	$x < 60$	2
B	$60 \leq x < 75$	5
C	$75 \leq x < 90$	a
D	$x \geq 90$	12

无人机飞行的时间/ $m i n$	0.5	1.5	3	5	7
无人机飞行的高度/ $m$	10			40

成绩（分）	20	30	40	50	60	70	90	100
频数（人）	1	3	3	9	8	4	3	4