广东省阳江市阳春市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-10-21 类型:期末考试
一、单选题
-
1. 下列根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 一本笔记本5元,买本共付元,则5和分别是( )A、常量,常量 B、变量,变量 C、常量,变量 D、变量,常量3. 如图,在平行四边形ABCD中,∠A=150°,则∠C的度数是( )
 A、30° B、75° C、100° D、150°4. 下列运算正确的是( ).A、 B、 C、 D、5. 直角三角形两直角边长为6和8,则此三角形斜边上的中线的长是( )A、10 B、5 C、4 D、36. 在脱贫攻坚工作中,为比较甲、乙两村扶贫攻坚工作的成效,从这两村中,各随机抽取20户对其年收入情况进行调查.统计结果是两村年人均收入的平均数相同,方差分别是S甲2=6000,S乙2=480,则年人均收入比较均衡的村是( )A、甲村 B、乙村 C、甲、乙两村一样 D、无法确定7. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )A、
A、30° B、75° C、100° D、150°4. 下列运算正确的是( ).A、 B、 C、 D、5. 直角三角形两直角边长为6和8,则此三角形斜边上的中线的长是( )A、10 B、5 C、4 D、36. 在脱贫攻坚工作中,为比较甲、乙两村扶贫攻坚工作的成效,从这两村中,各随机抽取20户对其年收入情况进行调查.统计结果是两村年人均收入的平均数相同,方差分别是S甲2=6000,S乙2=480,则年人均收入比较均衡的村是( )A、甲村 B、乙村 C、甲、乙两村一样 D、无法确定7. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )A、 B、
B、 C、
C、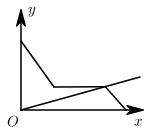 D、
D、 8. 在一次数学测验中,小明成绩80分,超过班级半数同学的成绩,分析得出这个的结论所用的统计量是( )A、平均数 B、中位数 C、众数 D、方差9. 已知正比例函数的函数图象如图所示,则一次函数的图象大致是( )
8. 在一次数学测验中,小明成绩80分,超过班级半数同学的成绩,分析得出这个的结论所用的统计量是( )A、平均数 B、中位数 C、众数 D、方差9. 已知正比例函数的函数图象如图所示,则一次函数的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 下列说法中能推出△ABC是直角三角形的个数有( )
10. 下列说法中能推出△ABC是直角三角形的个数有( )①a2=c2+b2 , ②∠A∶∠B∶∠C=1∶1∶2,③a∶b∶c=∶∶ , ④∠C=∠A
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 函数y=的自变量x的取值范围是 .
12. 点A(1,m),B(2,n)是直线y=﹣3x上的两点,则mn.(填<,>或=)13. 如图,D,E,F分别为△ABC三边的中点,则图中平行四边形的个数为.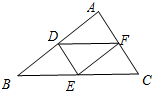 14. 分母有理化:= .15. 菱形的两条对角线长分别为5和8,则这个菱形的面积为 .16. 某公司招聘一名技术人员,对小宇进行了面试和笔试,面试和笔试的成绩分别为80分和90分,综合成绩按照面试占40%,笔试占60%进行计算,则小宇的综合成绩为分.17. 如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,AC=6,则点A的坐标是 .
14. 分母有理化:= .15. 菱形的两条对角线长分别为5和8,则这个菱形的面积为 .16. 某公司招聘一名技术人员,对小宇进行了面试和笔试,面试和笔试的成绩分别为80分和90分,综合成绩按照面试占40%,笔试占60%进行计算,则小宇的综合成绩为分.17. 如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,AC=6,则点A的坐标是 .
三、解答题
-
18. 计算:19. 已知y与2x﹣1成正比例,当x=3时,y=10,求y与x之间的函数关系式.20. 已知直角三角形的两直角边长分别为(2+)和(﹣2).(1)、求这个直角三角形的面积.(2)、求这个直角三角形的斜边长.21. 如图,在平行四边形ABCD中,E,F两点在对角线BD上,且 , 连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.
 22. 如图,在中, , 点D是AB靠近点B的四等分点,且 . 求证: .
22. 如图,在中, , 点D是AB靠近点B的四等分点,且 . 求证: . 23. 我校举行“中国梦·校园好声音”歌手大赛,初一、初二年级组根据年级初赛成绩,各选出5名选手参加学校总决赛,两个队各选出的5名选手的决赛成绩如图所示.
23. 我校举行“中国梦·校园好声音”歌手大赛,初一、初二年级组根据年级初赛成绩,各选出5名选手参加学校总决赛,两个队各选出的5名选手的决赛成绩如图所示. (1)、根据图示填写表格.
(1)、根据图示填写表格.平均数(分)
中位数(分)
众数(分)
初一组
85
85
初二组
80
(2)、结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?24. 如图,一次函数的图象与x轴交于点D,一次函数的图象与x轴交于点A,且经过点 , 两函数图象交于点 . (1)、求一次函数的解析式.(2)、根据图象,直接写出关于x的不等式的解集.25. 如图1,在△ABC中,∠B=90°,∠C=30°,点D从C点出发沿着CA方向以2个单位每秒的速度向终点A运动,同时点E从点A出发沿AB方向以1个单位每秒的速度向终点B运动.设点D,E的运动时间为t秒,DF⊥BC于F.
(1)、求一次函数的解析式.(2)、根据图象,直接写出关于x的不等式的解集.25. 如图1,在△ABC中,∠B=90°,∠C=30°,点D从C点出发沿着CA方向以2个单位每秒的速度向终点A运动,同时点E从点A出发沿AB方向以1个单位每秒的速度向终点B运动.设点D,E的运动时间为t秒,DF⊥BC于F. (1)、求证:AE=DF;(2)、如图2,连接EF,AC=12.
(1)、求证:AE=DF;(2)、如图2,连接EF,AC=12.①是否存在t,使得四边形AEFD为菱形?若存在,求出t的值;若不存在,请说明理由;
②连接DE,当△DEF是直角三角形时,求t的值.