广东省深圳市龙岗区七校2021-2022学年八年级下学期期末考试数学试题

试卷更新日期：2022-10-21 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{2}{x - 3}$ 有意义，则x的取值应满足（）

A、x＝3 B、x＜3 C、x＞3 D、x≠3

查看试题解析
2. 下列是四届冬奥会会徽的部分图案，其中既是轴对称图形，又是中心对称图形的是（）.

A、1984前南斯拉夫 B、1988加拿大 C、2006意大利 D、2022中国

查看试题解析
3. 在下列不等式中，解集为 $x > - 1$ 的是（）

A、 $2 x > 2$ B、 $- 2 x > - 2$ C、 $2 x < - 2$ D、 $- 2 x < 2$

查看试题解析
4. 下列各式从左到右的变形中，属于因式分解的是（）

A、6x²y＝2x•3xy B、x²+4x+1＝x（x+4）+1 C、x³﹣2xy＝x（x²﹣2y） D、（a+3）（a﹣3）＝a²﹣9

查看试题解析
5. 每年的6月18日是京东店庆日，在店庆时京东都会推出一系列的大型促销活动．某布偶的成本为50元，定价为80元，为使得利润率不低于28%，在实际售卖时该布偶最多可以打（）折．

A、8.5 B、8 C、7.5 D、7

查看试题解析
6. 在△ABC中，分别以点B和点C为圆心，大于 $\frac{1}{2}$ BC长为半径画弧，两弧相交于点M，N．作直线MN，交AC于点D，交BC于点E，连接BD．若AB＝12，AC＝19，则△ABD的周长为（）

A、30 B、31 C、24 D、38

查看试题解析
7. 如图，在△ABC中，∠C＝90°，AP是角平分线，AB＝5，CP＝2，则△APB的面积为（）

A、5 B、10 C、20 D、12

查看试题解析
8. 如图所示，在平行四边形ABCD中，E为边AD上一点，将△DEC沿CE翻折得到△FEC，点F在AC上，且满足AF＝EF．若∠D＝48°，则∠ACE为（）．

A、59° B、54° C、52° D、48°

查看试题解析
9. 如图，点E是等边三角形△ABC边AC的中点，点D是直线BC上一动点，连接ED，并绕点E逆时针旋转90°，得到线段EF，连接DF．若运动过程中AF的最小值为 $\sqrt{3} + 1$ ，则AB的值为（）

A、2 B、 $4 \sqrt{3}$ C、 $2 \sqrt{3}$ D、4

查看试题解析
10. 如图，平行四边形ABCD中，对角线AC、BD相交于点O，若AB＝4，BC＝6，∠ABC＝60°，则图中阴影部分的面积为（）

A、3 B、 $3 \sqrt{3}$ C、 $12 \sqrt{3}$ D、6

查看试题解析

二、解答题

11.

(1)、分解因式： $x^{2} y - 2 x y^{2} + y^{3}$

(2)、解分式方程： $\frac{x}{2 x - 5} + \frac{4}{5 - 2 x} = 1$

查看试题解析
12. 解不等式组 ${\begin{array}{l} 5 x - 6 \leq 3 x \\ \frac{x - 2}{3} < \frac{x + 1}{2} - 1 \end{array}$ ，并把不等式组的解集表示在数轴上．

查看试题解析
13. 先化简再求值 $(\frac{x^{2}}{x + 2} - x + 2) \div \frac{x^{2} - 4}{x^{2} + 4 x + 4}$ ，选择一个你喜欢的x的值代入其中并求值．

查看试题解析
14. 在等腰△ABC中，AB＝AC，D、E分别为AB、BC边上的中点，连接DE并延长DE到F，使得EF＝2ED，连接AE、CF．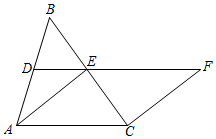

(1)、求证：四边形AEFC为平行四边形．

(2)、若AC＝5，BC＝6，求CF的长．

查看试题解析
15. 为实行乡村振兴计划，某县的果蔬加工公司先后两次购买龙眼，第一次购买龙眼用了56000元；因龙眼大量上市，价格下跌，该公司第二次购买龙眼用了84000元，所购进数量是第一次的2倍，但进货单价比第一次便宜了2000元/吨．

(1)、求该公司第一次购进龙眼多少吨？

(2)、公司计划把两次购买的龙眼加工成龙眼肉和干龙眼，1吨龙眼可加工成龙眼肉0.2吨或干龙眼0.5吨，龙眼肉和干龙眼的销售价格分别是10万元/吨和3万元/吨，若全部的销售额不少于39万元，则至少需要把多少吨龙眼加工成龙眼肉？

查看试题解析
16. 龙岗区八年级某班级在探究“将军饮马问题”时抽象出数学模型：直线l同旁有两个定点A、B，在直线l上存在点P，使得PA+PB的值最小．
解法：如图1，作点A关于直线l的对称点A′，连接A′B，则A′B与直线l的交点即为P，且PA+PB的最小值为A′B．
请利用上述模型解决下列问题：

(1)、格点应用：如图2，边长为1的正方形网格内有两点A、B，直线l与A、B的位置如图所示，点P是直线l上一动点，则PA+PB的最小值为；

(2)、几何应用：如图3，△ABC中，∠C＝90°，AC＝4，BC＝6，E是AB的中点，P是BC边上的一动点，则PA+PE的最小值为；

(3)、代数应用：代数式 $\sqrt{x^{2} + 4} + \sqrt{(6 - x)^{2} + 36}$ （0≤x≤6）的最小值为；

查看试题解析
17. 如图

(1)、如图1，△ABC为等边三角形，点D为BC边上的一动点（点D不与B、C重合），以AD为边作等边△ADE，连接CE．易求∠DCE＝°；

(2)、如图2，在△ABC中，∠BAC＝90°，AC＝AB，点D为BC上的一动点（点D不与B、C重合），以AD为边作等腰Rt△ADE，∠DAE＝90°（顶点A、D、E按逆时针方向排列），连接CE，类比题（1），请你猜想：线段BD、CD、DE之间的关系，并说明理由；

(3)、如图3，在（2）的条件下，若D点在BC的延长线上运动，以AD为边作等腰Rt△ADE，∠DAE＝90°（顶点A、D、E按逆时针方向排列），连接CE．CE＝10，BC＝6，求AE的长．

查看试题解析

三、填空题

18. 分解因式： $a^{2} - 2 a$ ＝．

查看试题解析
19. 如图，已知一次函数y＝kx+b的图象经过点A（﹣3，2），B（1，0），则关于x的不等式kx+b＜2解集为．

查看试题解析
20. 若关于x的分式方程 $\frac{a}{x - 3} + \frac{2}{3 - x} = 4$ 有增根，则a的值为．

查看试题解析
21. 在平面直角坐标系中，A（3，2），B（﹣1，﹣4），C在y轴上，D在x轴上，若以A，B，C，D四点为顶点的四边形是平行四边形，则点D的坐标为．

查看试题解析
22. 如图，△ABC中，∠BAC＝120°，AB＝AC，点D为BC边上一点．点E为线段CD上一点，且CE＝2，AB＝ $4 \sqrt{3}$ ， ∠DAE＝60°，则DE的长为．

查看试题解析