广东省汕头市金平区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-10-21 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{0.6}$ C、 $\sqrt{8}$ D、 $\sqrt{15}$

查看试题解析
2. 在下列以线段a、b、c的长为三边的三角形中，不能构成直角三角形的是（）

A、 $a ： b ： c = 3 ： 4 ： 5$ B、 $a = 1.5$ ， $b = 2$ ， $c = 3$ C、 $a = 7$ ， $b = 24$ ， $c = 25$ D、 $a = 9$ ， $b = 12$ ， $c = 15$

查看试题解析
3. 广东省今年5月15日部分城市的最高气温如表：
市
广州
深圳
佛山
汕头
珠海
东莞
中山
湛江
最高气温
23
23
22
21
24
23
24
26
则这8个市区该日最高气温的众数和中位数分别是（）

A、23，23 B、23，23.5 C、24，23 D、24，24

查看试题解析
4. 已知 $(1 ， y_{1})$ 、 $(2 ， y_{2})$ 是直线y＝2x＋1上的两点，则 $y_{1}$ ， $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、无法比较

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{2} \times \sqrt{6} = 2 \sqrt{6}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{40} \div \sqrt{5} = 2 \sqrt{2}$ D、 $\sqrt{{(- 12)}^{2}} = - 12$

查看试题解析
6. 如图，平行四边形ABCD中，∠ABC的平分线BE交AD于E，AB＝4，BC＝9，则DE的长（）

A、4 B、5 C、6.5 D、6

查看试题解析
7. 如图，已知函数 $y = (k - 1) x + k$ 的图象经过二、三、四象限，则k的取值范围是（）

A、 $k < 0$ B、 $k < 1$ C、 $0 < k < 1$ D、 $k > 1$

查看试题解析
8. 已知数据1，2，3，3，4，5，则下列关于这组数据的说法错误的是（）

A、众数是3 B、平均数是3 C、方差是2 D、中位数是3

查看试题解析
9. 放寒假了，乐乐骑车从家去外婆家玩，先前进了a千米，在路上遇到同学培培.停下来闲聊了一会，乐乐发现数学卷子忘在了学校，于是借了培培的卷子返回路过的打印店去复印，原路原速返回了b千米（b<a），再掉头沿原方向加速行驶，则乐乐离家的距离s与时间t的函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在矩形ABCD中，点E，F分别是边AB，BC的中点，连接EC，FD，点H，G分别是EC，FD的中点，连接GH，若AB＝6，BC＝8，则GH的长度为（）

A、2 B、 $\frac{5}{2}$ C、 $\frac{\sqrt{73}}{2}$ D、5

查看试题解析

二、填空题

11. 要使式子 $\sqrt{2 x - 14}$ 有意义，则x的取值范围是．

查看试题解析
12. 把直线y＝2x向上平移5个单位得到直线l，则直线l的解析式为．

查看试题解析
13. “杂交水稻之父”袁隆平为提高水稻的产量贡献了自己的一生．某研究员随机从甲、乙两块试验田中各抽取100株杂交水稻苗测试高度，计算平均数和方差的结果为 ${\bar{x}}_{甲} = 12$ ， ${\bar{x}}_{乙} = 12$ ， $s_{甲}^{2} = 4.2$ ， $s_{乙}^{2} = 3.3$ ，则杂交水稻长势比较整齐的是．

查看试题解析
14. 小璐的笔试成绩为95分，面试成绩为90分，若笔试成绩、面试成绩按6：4算平均成绩，则小璐的平均成绩是分．

查看试题解析
15. 某小区两面直立的墙壁之间为安全通道，一架梯子斜靠在左墙DE时，梯子底端A到左墙的距离AE为0.7m，梯子顶端D到地面的距离DE为2.4m，若梯子底端A保持不动，将梯子斜靠在右墙BC上，梯子顶端C到地面的距离CB为2m，则这两面直立墙壁之间的安全通道的宽BE为m．

查看试题解析
16. 如图，已知菱形 $A B C D$ 的面积为24，正方形 $A E C F$ 的面积为18，则菱形的边长是．

查看试题解析
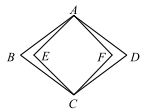17. 如图，在直角坐标系中，直线 $y = 2 x + 4$ 分别交 $x$ 轴， $y$ 轴于A，B两点，C为OB的中点，点D在第二象限，且四边形AOCD为矩形，P是CD上一个动点，过点P作PH⊥OA于H，Q是点B关于点A的对称点，则BP＋PH＋HQ的最小值为．

查看试题解析

三、解答题

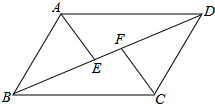
18. 计算： $\sqrt{27} - \sqrt{12} \div \sqrt{3} - 3 \sqrt{\frac{1}{3}} + {(- \sqrt{7})}^{2}$

查看试题解析
19. 如图，在平行四边形ABCD中，E，F分别是对角线BD上的两点，且BE＝DF.求证：AE＝CF.

查看试题解析
20. 如图，一高层住宅发生火灾，消防车立即赶到距大厦8米（AC的长）处，升起云梯到火灾窗口，云梯AB长17米，云梯底部距地面3米（AE的长），问：发生火灾的住户窗口距离地面有多高（BD的长）？

查看试题解析
21. 金平区为了加强社区居民对防疫的了解，通过网络宣传防疫知识，并鼓励社区居民在线参与作答《2022防疫知识》模拟试卷，社区工作人员随机从甲、乙两个社区各抽取20名人员的答卷成绩，并对他们的成绩（单位：分）进行统计、分析，过程如下：
收集数据
甲区：80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
乙区：85 80 95 100 90 95 85 65 75 85 89 90 70 90 100 80 80 90 96 75
整理数据
成绩x（分）
$60 \leq x \leq 70$
$70 < x \leq 80$
$80 < x \leq 90$
$90 < x \leq 100$
甲区
3
7
5
5
乙区
2
5
a
b
分析数据
统计量
平均数
中位数
众数
甲区
83.5
c
8
乙区
85.75
87
d
应用数据

(1)、填空：a＝， b＝， c＝， d＝；

(2)、若甲区共有1000人参与答卷，请估计甲区成绩大于80分的人数；

(3)、根据以上数据分析，你认为甲、乙两个区哪一个对防疫知识掌握更好？请写出理由．

查看试题解析
22. 如图，网格是由小正方形拼成，每个小正方形的边长都为1．四边形ABCD的四个点都在格点上．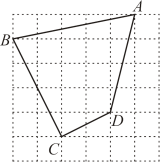

(1)、四边形ABCD的面积为，周长为；

(2)、求证：∠BCD是直角；

查看试题解析
23. 凤凰单丛（枞）茶，是潮汕的名茶，已有九百余年的历史．潮汕人将单丛茶按香型分为黄枝香、芝兰香、桃仁香、玉桂香、通天香、鸭屎香等多种．清明采茶季后，某茶叶店准备购买通天香和鸭屎香两种单丛茶进行销售，已知若购买4千克通天香单丛和3千克鸭屎香单丛需要2500元，购买2千克通天香单丛和5千克鸭屎香单丛需要2300元．

(1)、求通天香、鸭屎香两种茶叶的单价分别为多少元？

(2)、茶叶专卖店计划购买通天香、鸭屎香两种单丛茶共80千克，总费用不多于26000元，并且要求通天香茶叶数量不能低于10千克，那么应如何安排购买方案才能使总费用最少，最少费用应为多少元？

查看试题解析
24. 已知：在边长为6的正方形ABCD中，点P为对角线BD上一点，且 $B P = 4 \sqrt{2}$ ．将三角板的直角顶点与点P重合，一条直角边与直线BC交于点E，另一条直角边与射线BA交于点F（点F不与点B重合），将三角板绕点P旋转．

(1)、如图，当点E、F在线段BC、AB上时，求证：PE＝PF；

(2)、当∠FPB＝60°时，求△ BEP的面积；

(3)、当△ BEP为等腰三角形时，直接写出线段BF的长．

查看试题解析
25. 如图，在平面直角坐标系中，直线AB的解析式为 $y = - \frac{1}{3} x + 4$ ，它与x轴交于点B，与y轴交于点A，直线y＝x与直线AB交于点C．动点P从点C出发，以每秒1个单位长度的速度沿射线CO运动，运动时间为t秒．

(1)、求△ AOC的面积；

(2)、设△ PAC的面积为S，求S与t的函数关系式；

(3)、M是直线OC上一点，在平面内是否存在点N，使以A，O，M，N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析

市	广州	深圳	佛山	汕头	珠海	东莞	中山	湛江
最高气温	23	23	22	21	24	23	24	26

成绩x（分）	$60 \leq x \leq 70$	$70 < x \leq 80$	$80 < x \leq 90$	$90 < x \leq 100$
甲区	3	7	5	5
乙区	2	5	a	b

统计量	平均数	中位数	众数
甲区	83.5	c	8
乙区	85.75	87	d