广东省广州市越秀区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-10-21 类型:期末考试
一、单选题
-
1. 若代数式 在实数范围内有意义,则 的取值范围是A、x<1 B、x≤1 C、x>1 D、x≥12. 在下列各式中,最简二次根式是( )A、 B、 C、 D、3. 点(a,﹣1)在一次函数y=﹣2x+1的图象上,则a的值为( )A、a=﹣3 B、a=﹣1 C、a=1 D、a=24. 如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长为( )
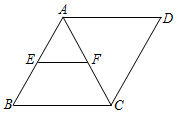 A、24 B、18 C、12 D、95. 下列计算正确的是( )A、 B、 C、 D、6. 2022年2月,第24届冬季奥林匹克运动会在北京举行.某校八年级(1)班在班会课开展了冬奥会知识小竞赛,10位同学在这个知识竞赛中的成绩统计结果如表所示,则这10位同学的平均成绩是( )
A、24 B、18 C、12 D、95. 下列计算正确的是( )A、 B、 C、 D、6. 2022年2月,第24届冬季奥林匹克运动会在北京举行.某校八年级(1)班在班会课开展了冬奥会知识小竞赛,10位同学在这个知识竞赛中的成绩统计结果如表所示,则这10位同学的平均成绩是( )成绩
7
8
9
10
人数
1
4
3
2
A、8 B、8.5 C、8.6 D、97. 若函数和函数的图象如图所示,则关于x的不等式的解集是( )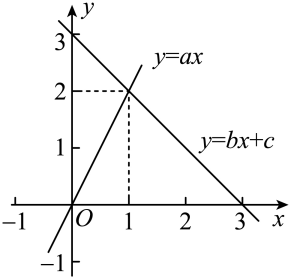 A、 B、 C、 D、8. 如图,在平行四边形ABCD中,于点E,于点F,若 , 则( )
A、 B、 C、 D、8. 如图,在平行四边形ABCD中,于点E,于点F,若 , 则( ) A、 B、 C、 D、9. 若点 , 都在直线上,则下列大小关系成立的是( ).A、 B、 C、 D、10. 在平面直角坐标系xOy中,直线过定点P,过点A(6,m)作直线轴交直线于点B,连接OB,若BP平分 , 则k的值是( )A、 B、 C、 D、
A、 B、 C、 D、9. 若点 , 都在直线上,则下列大小关系成立的是( ).A、 B、 C、 D、10. 在平面直角坐标系xOy中,直线过定点P,过点A(6,m)作直线轴交直线于点B,连接OB,若BP平分 , 则k的值是( )A、 B、 C、 D、二、填空题
-
11. = .12. 将函数y=2x+1的图象向上平移2个单位,所得的函数图象的解析式为 .13. 甲、乙两人进行射击测试,每个人10次射击成绩的平均值都是8.5环,方差分别是 , , 则两人中成绩比较稳定的是 . (填“甲”或“乙”)14. 已知 , 则代数式的值是 .15. 如图,在直线l上摆放着三个正方形,其中正放的两个正方形的顶点M,N分别是斜放正方形相邻两边的中点,三个正方形的面积依次为 , , . 已知 , , 则= .
 16. 如图,正方形ABCD的边长为4,点E为对角线BD上任意一点(不与B,D重合),连接AE,过点E作 , 交线段BC于点F,以AE,EF为邻边作矩形AEFG,连接BG.给出下列四个结论:
16. 如图,正方形ABCD的边长为4,点E为对角线BD上任意一点(不与B,D重合),连接AE,过点E作 , 交线段BC于点F,以AE,EF为邻边作矩形AEFG,连接BG.给出下列四个结论:①;②;
③设四边形AGBE的周长为m,则;
④当时,的面积为3.
其中正确的结论有 . (填写所有正确结论的序号)

三、解答题
-
17. 计算:18. 已知:如图,在ABCD中,点E、F分别在AD、BC上,且∠ABE=∠CDF.
求证:四边形BFDE是平行四边形.
 19. 如图,已知 , ,
19. 如图,已知 , , (1)、求AB的长;(2)、求的面积.20. 新冠肺炎疫情防控时刻不能放松.某校倡议学生积极参加体育锻炼,提高免疫力.为了解八年级学生周末体育锻炼的情况,在该校八年级学生中随机抽取了16名女生和16名男生,调查了他们周末的锻炼时间,收集到如下数据(单位:分钟)
(1)、求AB的长;(2)、求的面积.20. 新冠肺炎疫情防控时刻不能放松.某校倡议学生积极参加体育锻炼,提高免疫力.为了解八年级学生周末体育锻炼的情况,在该校八年级学生中随机抽取了16名女生和16名男生,调查了他们周末的锻炼时间,收集到如下数据(单位:分钟)女生
49
56
67
68
72
76
78
79
80
80
90
95
99
103
108
115
男生
58
65
66
72
75
79
79
82
83
88
94
98
102
108
113
124
(1)、女生锻炼时间的众数为 , 男生锻炼时间的中位数为;(2)、如果该校八年级的女生有128人,男生有144人,请估计该校八年级学生周末锻炼时间在100分钟以上(不包含100分钟)的人数.21. 在中, . 点D是边AB上的一点,连接CD.作 , , 连接ED.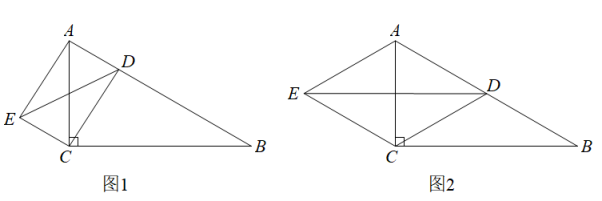 (1)、如图1,当时,求证:;(2)、如图2,当D是边AB的中点时,若 , , 求四边形ADCE的面积.22. A,B两地距离24km,甲、乙两人同时从A地出发前往B地.甲先匀速慢走2h,而后匀速慢跑;乙始终保持匀速快走,设运动时间为x(单位:h).甲、乙距离A地的路程分别为 , (单位:km), , 分别与x的函数关系如图所示.
(1)、如图1,当时,求证:;(2)、如图2,当D是边AB的中点时,若 , , 求四边形ADCE的面积.22. A,B两地距离24km,甲、乙两人同时从A地出发前往B地.甲先匀速慢走2h,而后匀速慢跑;乙始终保持匀速快走,设运动时间为x(单位:h).甲、乙距离A地的路程分别为 , (单位:km), , 分别与x的函数关系如图所示.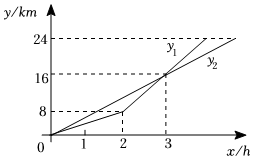 (1)、求关于x的函数解析式;(2)、相遇前,是否存在甲、乙两人相距1km的时刻?若存在,求运动时间;若不存在,请说明理由.23. 如图,已知 .
(1)、求关于x的函数解析式;(2)、相遇前,是否存在甲、乙两人相距1km的时刻?若存在,求运动时间;若不存在,请说明理由.23. 如图,已知 . (1)、尺规作图:作平行四边形ABCD;(保留作图痕迹,不写作法.)(2)、在(1)所作的平行四边形ABCD中,连接BD,交AC于点O.
(1)、尺规作图:作平行四边形ABCD;(保留作图痕迹,不写作法.)(2)、在(1)所作的平行四边形ABCD中,连接BD,交AC于点O.①若 , , , 求BD的长;
②过点O作直线EF与边AD,BC分别交于点E,F,设四边形EDCF的面积为 , 平行四边形ABCD的面积为 , 求的值.
24. 如图,点A(0,2),B(3,3), , 四边形OBCD是矩形,BD与x轴交于点E. (1)、求直线AB的解析式;(2)、求线段OE的长;(3)、若点P为直线AB上一动点,设的面积为 , 的面积为 , 且 , 求点P的坐标.25. 已知 , , 点C为射线BF上一动点(不与点B重合),关于AC的轴对称图形为 .
(1)、求直线AB的解析式;(2)、求线段OE的长;(3)、若点P为直线AB上一动点,设的面积为 , 的面积为 , 且 , 求点P的坐标.25. 已知 , , 点C为射线BF上一动点(不与点B重合),关于AC的轴对称图形为 . (1)、如图1,当点D在射线AE上时,求证;四边形ABCD是菱形;(2)、如图2,当点D在射线AE,BF之间时,若点G为射线BF上一点,点C为BG的中点,且 , , 求DG的长;(3)、如图3,在(1)的条件下,若 , 连接BD,点P,Q分别是线段BC,BD上的动点,且 , 求的最小值.
(1)、如图1,当点D在射线AE上时,求证;四边形ABCD是菱形;(2)、如图2,当点D在射线AE,BF之间时,若点G为射线BF上一点,点C为BG的中点,且 , , 求DG的长;(3)、如图3,在(1)的条件下,若 , 连接BD,点P,Q分别是线段BC,BD上的动点,且 , 求的最小值.