广东省广州市荔湾区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-10-21 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{8}$ B、 $\sqrt{a^{2} - b^{2}}$ C、 $\sqrt{\frac{1}{x - 1}}$ D、 $\sqrt{153}$

查看试题解析
2. 如果 $\sqrt{{(2 a - 1)}^{2}} = 1 - 2 a$ ，则a的取值范围是（）

A、 $a < \frac{1}{2}$ B、 $a \leq \frac{1}{2}$ C、 $a > \frac{1}{2}$ D、 $a \geq \frac{1}{2}$

查看试题解析
3. 若 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 2 x - 3 = 0$ 的两个根，则 $x_{1} + x_{2}$ 的值是（）

A、2 B、-2 C、4 D、-3

查看试题解析
4. 直线 $y = - 2 x + b$ 上有三个点 $(- 2.4, y_{1})$ ， $(- 1.5, y_{2})$ ， $(1.3, y_{3})$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{2} > y_{1} > y_{3}$

查看试题解析
5. 下列方差最大的一组数据是（）

A、6，6，6，6，6 B、5，6，6，6，7 C、4，5，6，7，8 D、3，3，6，9，9

查看试题解析
6. 如图，在Rt△ABC中，∠A＝30°，BC＝1，点D，E分别是直角边BC，AC的中点，则DE的长为（）

A、1 B、2 C、 $\sqrt{3}$ D、1＋ $\sqrt{3}$

查看试题解析
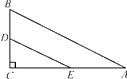7. 已知 $x = 1$ 是一元二次方程 $(m - 2) x^{2} + 4 x - m^{2} = 0$ 的一个根，则m的值为（）

A、-1或2 B、-1 C、2 D、0

查看试题解析
8. 关于函数 $y = - 2 x + 1$ ，下列结论正确的是（）

A、图象必经过点 $(- 2, 1)$ B、图象经过第一、二、三象限 C、当 $x > \frac{1}{2}$ 时， $y < 0$ D、y随x的增大而增大

查看试题解析
9. 如果直角三角形斜边上的中线和高分别是6和5，那么它的面积是（）

A、10 B、15 C、20 D、30

查看试题解析
10. 如图，点E是菱形ABCD对角线BD上任一点，点F是CD上任一点，连接CE，EF，当 $∠ A B C = 4 5^{°}$ ， $B C = 10$ 时， $C E + E F$ 的最小值是（）

A、 $10 \sqrt{2}$ B、10 C、 $5 \sqrt{2}$ D、5

查看试题解析

二、填空题

11. 若 ${(a - 3)}^{2} + \sqrt{b + 2} = 0$ ，则 $a + b =$ .

查看试题解析
12. 在直线坐标系中，点 $P (- 3 ， 5)$ 到原点的距离是．

查看试题解析
13. 若关于x的一元二次方程 $x^{2} + x - m = 0$ 有两个实数根，则m的取值范围是．

查看试题解析
14. 已知一组数据2、a、6、9、12的平均数为7，则a= ．

查看试题解析
15. 如果将直线 $y = 2 x$ 向右平移3个单位，那么所得直线与坐标轴所围成的三角形面积等于．

查看试题解析
16. 已知：如图，正方形ABCD中，AB=2，AC，BD相交于点O，E，F分别为边BC，CD上的动点（点E，F不与线段BC，CD的端点重合）且BE=CF，连接OE，OF，EF．在点E，F运动的过程中，有下列四个结论：
①△OEF是等腰直角三角形；
②△OEF面积的最小值是 $1$ ；
③至少存在一个△ECF，使得△ECF的周长是 $2 + \sqrt{3}$ ；
④四边形OECF的面积是1．
所有正确结论的序号是

查看试题解析

三、解答题

17. 解方程： $x (x - 2) = 3 x - 6$ ．

查看试题解析
18. 如图，在菱形ABCD中，AC，BD相交于点O，过B，C两点分别作AC，BD的平行线，相交于点E，求证：四边形BOCE是矩形．

查看试题解析
19. 计算：

(1)、 $\sqrt{18} - \sqrt{32} + \sqrt{2}$ ；

(2)、 $(3 \sqrt{2} - 2 \sqrt{3}) \times \sqrt{3} + {(\sqrt{2} - \sqrt{3})}^{2}$ ．

查看试题解析
20. 如图，过点A（1，0）的两条直线 $l_{1}$ ， $l_{2}$ 分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知 $A B = \sqrt{10}$ ．

(1)、求点B的坐标；

(2)、若△ABC的面积是3，求直线 $l_{2}$ 的解析式．

查看试题解析
21. 已如：如图，四边形 $A B C D$ 中， $∠ B = 90 ° ， A B = 3 ， B C = 4 ， C D = 12 ， A D = 13$ ，求四边形 $A B C D$ 的面积．

查看试题解析
22. 某乡镇企业生产部有技术工人15人，生产部为了合理计划产品的月生产定额，统计这15人某月加工零件个数如下：
加工零件个数（个）
540
450
300
240
210
120
人数（人）
1
1
2
6
3
2

(1)、写出15人该月加工零件个数的平均数、中位数和众数；

(2)、假设生产部负责人把每位工人的月加工零件个数定为260，你认为是否合理？为什么？若不合理，请你设定一个较为合理的定额，并说明理由．

查看试题解析
23. 一商店销售某种商品，平均每天可售出12件，每件盈利20元．为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于15元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．

(1)、若每件商品降价2元，则平均每天盈利多少元？

(2)、当每件商品降价多少元时，该商店每天的盈利为320元？

查看试题解析
24. 如图，在平面直角坐标系中， $O$ 为坐标原点，矩形 $O A B C$ 的顶点 $A (8 ， 0)$ ， $C (0 ， 6)$ ，将矩形 $O A B C$ 的一个角沿直线 $B D$ 折叠，使得点 $A$ 落在对角线 $O B$ 上的点 $E$ 处，折痕与 $x$ 轴交于点 $D$ ．

(1)、线段 $O B$ 的长度；

(2)、求直线 $B D$ 所对应的函数表达式；

(3)、若点 $Q$ 在线段 $B D$ 上，在线段 $B C$ 上是否存在点 $P$ ，使以 $D$ ， $E$ ， P， $Q$ 为顶点的四边形是平行四边形？若存在，请求出点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析
25. 如图， $△ A B C$ 为等边三角形，四边形BCDE为正方形， $A B = 6$ ，点M以每秒1个单位的速度从点A沿AC向点C运动，同时点N以同样的速度从点D沿DE向点E运动，当点M达到点C时，M，N同时停止运动，设点M的运动时间为t．

(1)、当 $t = 0$ 时，求 $∠ C M N$ 的度数；

(2)、若 $∠ C M N = 60 °$ ，求线段MN的长；

(3)、当点M，N在运动时，求MN的最小值．

查看试题解析

加工零件个数（个）	540	450	300	240	210	120
人数（人）	1	1	2	6	3	2