广东省广州市番禺区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-10-21 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、=2 B、=﹣2 C、=2 D、=±22. 下列等式成立的是( )A、 B、 C、 D、3. 如图,正方形内的数字代表所在正方形的面积,则A所在的正方形的面积为( )
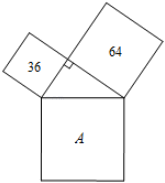 A、 B、28 C、128 D、1004. 关于菱形的性质,以下说法错误的是( )A、四条边相等 B、对角线相等 C、对角线互相垂直 D、是轴对称图形5. 直线y=kx+2过点(﹣1,4),则k的值是( )A、﹣2 B、﹣1 C、﹣ D、26. 数据3,4,6,6,5的中位数是( )A、4.5 B、5 C、5.5 D、67. 如图,直线y=x+5和直线y=ax+b相交于点P,观察其图象可知方程x+5=ax+b的解( )
A、 B、28 C、128 D、1004. 关于菱形的性质,以下说法错误的是( )A、四条边相等 B、对角线相等 C、对角线互相垂直 D、是轴对称图形5. 直线y=kx+2过点(﹣1,4),则k的值是( )A、﹣2 B、﹣1 C、﹣ D、26. 数据3,4,6,6,5的中位数是( )A、4.5 B、5 C、5.5 D、67. 如图,直线y=x+5和直线y=ax+b相交于点P,观察其图象可知方程x+5=ax+b的解( )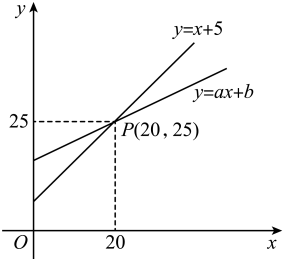 A、x=15 B、x=25 C、x=10 D、x=208. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、
A、x=15 B、x=25 C、x=10 D、x=208. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、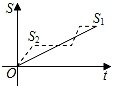 B、
B、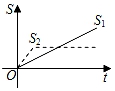 C、
C、 D、
D、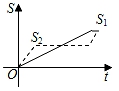 9. 如图,在▱ABCD中,BE平分∠ABC交DC于点E,若∠A=60°,则∠DEB的大小为( )
9. 如图,在▱ABCD中,BE平分∠ABC交DC于点E,若∠A=60°,则∠DEB的大小为( )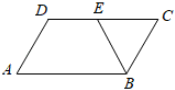 A、130° B、120° C、115° D、110°10. 如图,AB,BC,CD,DE是四根长度均为5cm的小木棒,点A、C、E共线.若AC=6cm,CD⊥BC,则线段CE的长度是( )
A、130° B、120° C、115° D、110°10. 如图,AB,BC,CD,DE是四根长度均为5cm的小木棒,点A、C、E共线.若AC=6cm,CD⊥BC,则线段CE的长度是( )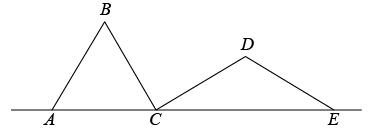 A、7cm B、6cm C、8cm D、8cm
A、7cm B、6cm C、8cm D、8cm二、填空题
-
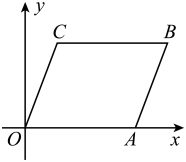
11. 计算 =.12. 如图,将▱ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(4,0),点C的坐标是(1,3),则点B的坐标是
 13. 将直线y=2x-1向上平移3个单位长度,则平移后直线的解析式为 .14. 如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AB长为半径作弧,交BC于点D,再分别以点B,D为圆心,以大于BD的长为半径作弧,两弧交于点P,作射线AP交BC于点E,如果AB=3,AC=4,那么线段AE的长度是
13. 将直线y=2x-1向上平移3个单位长度,则平移后直线的解析式为 .14. 如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AB长为半径作弧,交BC于点D,再分别以点B,D为圆心,以大于BD的长为半径作弧,两弧交于点P,作射线AP交BC于点E,如果AB=3,AC=4,那么线段AE的长度是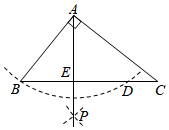 15. 如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,观察图形,设甲、乙这10次射击成绩的方差分别为S甲2 , S乙2 , 则S甲2S乙2(填“<”、“>”或“=”).
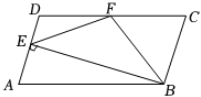
15. 如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,观察图形,设甲、乙这10次射击成绩的方差分别为S甲2 , S乙2 , 则S甲2S乙2(填“<”、“>”或“=”). 16. 如图,在 ▱ ABCD中,CD=2AD,F为DC的中点,BE⊥AD于点E,连接EF,BF,下列结论:
16. 如图,在 ▱ ABCD中,CD=2AD,F为DC的中点,BE⊥AD于点E,连接EF,BF,下列结论:①∠ABC=2∠ABF;
②EF=BF;
③S△ABE:S△EFB=2:3;
④∠CFE=3∠DEF.
其中正确结论的序号是 .
三、解答题
-
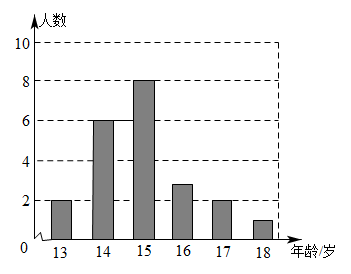
17. 计算:(1)、;(2)、()()﹣(﹣1)2 .18. 某校男子足球队的年龄分布如上面的条形图所示,请找出这些队员年龄的平均数、众数、中位数,并解释它们的意义.
 19. 设矩形的面积为S,相邻两边长分别为a、b,对角线长为l,已知S=2 , b= , 求a和l.20. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=1.5,BD=2.5.
19. 设矩形的面积为S,相邻两边长分别为a、b,对角线长为l,已知S=2 , b= , 求a和l.20. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=1.5,BD=2.5.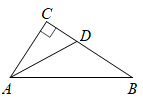 (1)、求点D到直线AB的距离;(2)、求线段AC的长.21. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,已知甲船沿北偏西37°方向航行,求乙船航行的方向.
(1)、求点D到直线AB的距离;(2)、求线段AC的长.21. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,已知甲船沿北偏西37°方向航行,求乙船航行的方向.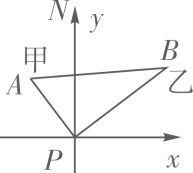 22. 如图,直线l:y=x+与两坐标轴分别交于A、B两点,点M为线段AB的中点,
22. 如图,直线l:y=x+与两坐标轴分别交于A、B两点,点M为线段AB的中点,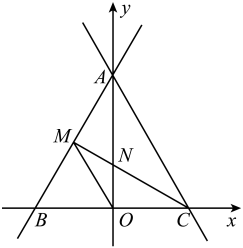 (1)、求A、B、M的坐标;(2)、直线l关于y轴对称的直线为l',写出直线l'的解析式;(3)、若直线l'交x轴于点C,直线MC与y轴的交点为N,连接OM,求 .23. 如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)、求A、B、M的坐标;(2)、直线l关于y轴对称的直线为l',写出直线l'的解析式;(3)、若直线l'交x轴于点C,直线MC与y轴的交点为N,连接OM,求 .23. 如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.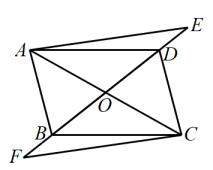 (1)、求证:△ADE≌△CBF;(2)、试连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.24. 已知A,B两地相距25km.甲8:00由A地出发骑电动自行车去B地,平均速度为20km/h;乙在8:15由A地出发乘汽车也去B地,平均速度为40km/h.(1)、分别写出两个人的行程关于时刻的函数解析式,在同一坐标系中画出函数的图象;(2)、乙能否在途中超过甲?如果能超过,请结合图象说明,何时超过?(3)、设甲、乙两人之间的距离为d,试写出关于时刻的函数解析式,并画出此函数的图象.25. 如图,已知一次函数y=﹣x+b的图象过点A(0,3),点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形OMPN的边上分别截取:OB=OM,MC=MP,OE=ON,ND=NP.
(1)、求证:△ADE≌△CBF;(2)、试连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.24. 已知A,B两地相距25km.甲8:00由A地出发骑电动自行车去B地,平均速度为20km/h;乙在8:15由A地出发乘汽车也去B地,平均速度为40km/h.(1)、分别写出两个人的行程关于时刻的函数解析式,在同一坐标系中画出函数的图象;(2)、乙能否在途中超过甲?如果能超过,请结合图象说明,何时超过?(3)、设甲、乙两人之间的距离为d,试写出关于时刻的函数解析式,并画出此函数的图象.25. 如图,已知一次函数y=﹣x+b的图象过点A(0,3),点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形OMPN的边上分别截取:OB=OM,MC=MP,OE=ON,ND=NP.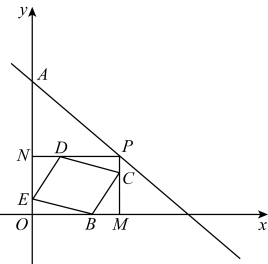 (1)、求b的值;(2)、求证:四边形BCDE是平行四边形;(3)、在直线y=﹣x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
(1)、求b的值;(2)、求证:四边形BCDE是平行四边形;(3)、在直线y=﹣x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.