北京市西城区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-10-21 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{0.25}$ D、 $\sqrt{10}$

查看试题解析
2. 如图，BD是 $▱ A B C D$ 的对角线，如果 $∠ A B C = 80 °$ ， $∠ A D B = 25 °$ ，则 $∠ B D C$ 等于（）

A、65° B、55° C、45° D、25°

查看试题解析
3. 下列计算，正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{8} + \sqrt{2} = \sqrt{10}$ C、 $3 \sqrt{2} - \sqrt{2} = 3$ D、 $\sqrt{(- 1) \cdot (- 1)} = 1$

查看试题解析
4. 下列命题中，正确的是（）

A、一组对边平行且另一组对边相等的四边形是平行四边形 B、两组邻边分别相等的四边形是平行四边形 C、两组对边分别平行的四边形是平行四边形 D、对角线互相垂直的四边形是平行四边形

查看试题解析
5. 在庆祝新中国成立70周年的校园歌唱比赛中，11名参赛同学的成绩各不相同，按照成绩取前5名进入决赛．如果小明知道了自己的比赛成绩，要判断能否进入决赛，小明需要知道这11名同学成绩的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 在△ABC中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别记为a，b，c，下列条件中，能判定△ABC是直角三角形的是（）

A、 $a^{2} = (c - b) (c + b)$ B、 $a = 1$ ， $b = 2$ ， $c = 3$ C、 $∠ A = ∠ C$ D、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$

查看试题解析
7. 如图，直线 $y = k_{1} x + b_{1}$ 和直线 $y = k_{2} x + b_{2}$ 相交于点 $M (\frac{2}{3} ， - 2)$ ，则关于x，y的方程组 ${\begin{array}{l} y = k_{1} x + b_{1} \\ y = k_{2} x + b_{2} \end{array}$ ，的解为（）

A、 ${\begin{array}{l} x = \frac{2}{3} ， \\ y = - 2 \end{array}$ B、 ${\begin{array}{l} x = - 2 ， \\ y = \frac{2}{3} \end{array}$ C、 ${\begin{array}{l} x = \frac{2}{3} ， \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = - 2 ， \\ y = - \frac{2}{3} \end{array}$

查看试题解析
8. 点P从某四边形的一个顶点A出发，沿着该四边形的边逆时针匀速运动一周．设点P运动的时间为x，点P与该四边形对角线交点的距离为y，表示y与x的函数关系的大致图像如图所示，则该四边形可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 若二次根式 $\sqrt{x + 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
10. 如图，在Rt $△ A B C$ 中，∠ACB=90°，点D是AB的中点，AC=6 ， BC=8，则CD= ．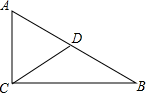

查看试题解析
11. 将函数 $y = 2 x$ 的图象沿y轴向下平移3个单位长度后，所得图象对应的函数表达式为．

查看试题解析
12. 如图，在△ABC中， $∠ C = 90 °$ ， $∠ A = 30 °$ ，点M，N分别为AC，BC的中点，连接MN．若 $B C = 2$ ，则MN的长度是．

查看试题解析
13. 在平面直角坐标系xOy中，菱形ABCD的四个顶点都在坐标轴上．若 $A (- 4 ， 0)$ ， $B (0 ， - 3)$ ，则菱形ABCD的面积是．

查看试题解析
14. 射击运动员小东10次射击的成绩（单位：环）：7.5，8，7.5，8.5，9，7，7，10，8.5，8．这10次成绩的平均数是8.1，方差是0.79，如果小东再射击一次，成绩为10环，则小东这11次成绩的方差0.79．（填“大于”、“等于”或“小于”）

查看试题解析
15. 关于函数 $y_{1} = 2 x - 1$ 和函数 $y_{2} = - x + m (m > 0)$ ，有以下结论：
①当 $0 < x < 1$ 时， $y_{1}$ 的取值范围是 $- 1 < y_{1} < 1$
② $y_{2}$ 随x的增大而增大
③函数 $y_{1}$ 的图像与函数 $y_{2}$ 的图像的交点一定在第一象限
④若点 $(a ， - 2)$ 在函数 $y_{1}$ 的图像上，点 $(b ， \frac{1}{2})$ 在函数 $y_{2}$ 的图像上，则 $a < b$
其中所有正确结论的序号是．

查看试题解析
16. 小明与小亮两人约定周六去博物馆参观学习．两人同时出发，小明乘车从甲地途径乙地到博物馆，小亮骑自行车从乙地到博物馆．已知甲地、乙地和博物馆在一条直线上，右图是两人分别与乙地的距离S（单位：km）与时间t（单位：min）的函数图象，在小明到达博物馆前，当两人相距1km时，t的值是．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{24} \div \sqrt{6} \times \sqrt{3}$ ；

(2)、 $(\sqrt{3} + 1) (\sqrt{3} - 1) + \sqrt{18}$ ．

查看试题解析
18. 已知：如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ．求作：矩形ABCD．
作法：①作线段AB的垂直平分线交AB于点O．
②作射线CO．
③以点O为圆心，线段CO长为半径画弧，交射线CO于点D．
④连接AD，BD，则四边形ACBD即为所求作的矩形．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：∵ $O A = O B$ ， ① $= O D$
∴四边形ACBD是平行四边形．（ ② ）（填推理的依据）
∵ $∠ A C B = 90 °$ ，
∴四边形ACBD是矩形．（ ③ ）（填推理的依据）

查看试题解析
19. 在平面直角坐标系xOy中，一次函数 $y = k x + b (k \neq 0)$ 的图像经过点 $(3 ， 0)$ 和 $(- 3 ， - 2)$ ．

(1)、求该一次函数的解析式；

(2)、在所给的坐标系中画出该一次函数图象，并求它的图像与坐标轴围成的三角形的面积．

查看试题解析
20. 如图，矩形ABCD的对角线交于点O，且 $D E ∥ A C$ ， $C E ∥ B D$ ．

(1)、求证：四边形OCED是菱形；

(2)、连接BE．若 $A B = 2$ ， $∠ B A C = 60 °$ ，求BE的长．

查看试题解析
21. 在平面直角坐标系xOy中，一次函数 $y = - 2 x + 2$ 图像与x轴、y轴分别相交于点A和点B．

(1)、求A，B两点的坐标；

(2)、点C在x轴上，若△ABC是以边AB为腰的等腰三角形，求点C的横坐标．

查看试题解析
22. 某校为了解该校七年级和八年级学生线上数学学习的情况，从这两个年级的学生中，各随机抽取了20名学生进行有关测试，获得了他们的成绩（百分制，且成绩均为整数），并对数据（成绩）进行了整理、描述和分析，下面给出了部分信息．
a．该校抽取的八年级学生测试成绩的数据的频数分布直方图如下（数据分为4组： $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ）：
b．该校抽取的八年级学生测试成绩在 $70 \leq x < 80$ 这一组的数据是：
70 70 74 74 75 75 75 76 77 78
c．该校抽取的七、八年级学生测试成绩的数据的平均数、中位数、众数如下：

平均数
中位数
众数
七年级
78
79.5
79
八年级
79
$m$
75
根据以上信息，回答下列问题：

(1)、写出表中m的值；

(2)、此次测试成绩80分及80分以上为优秀．
①记该校抽取的七年级学生中成绩优秀的人数是 $n_{1}$ ，抽取的八年级学生中成绩优秀的人数为 $n_{2}$ ，比较 $n_{1}$ ， $n_{2}$ 的大小，并说明理由；
②若该校七年级有200名学生，八年级有180名学生，假设该校七、八年级学生全部参加此次测试，估计该校七年级和八年级学生中成绩优秀的人数共有多少人．

查看试题解析
23. 对于函数 $y = | x | + b$ ，小明探究了它的图像及部分性质．下面是他的探究过程，请补充完整：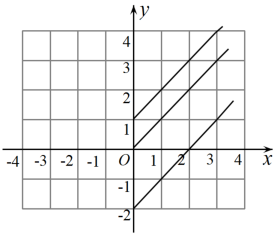

(1)、自变量x的取值范围是；

(2)、令b分别取0，1和 $- 2$ ，所得三个函数中的自变量与其对应的函数值如下表，则表中m的值是， n的值是；
$x$
…
-3
-2
-1
0
1
2
3
…
$y = | x |$
…
3
2
1
0
1
2
3
…
$y = | x | + 1$
…
4
$m$
2
1
2
3
4
…
$y = | x | - 2$
…
1
0
$n$
-2
-1
0
1
…

(3)、根据表中数据，补全函数 $y = | x |$ ， $y = | x | + 1$ ， $y = | x | - 2$ 的图像：

(4)、结合函数 $y = | x |$ ， $y = | x | + 1$ ， $y = | x | - 2$ 的图像，写出函数 $y = | x | + b$ 的一条性质：；

(5)、点 $(x_{1} ， y_{1})$ 和点 $(x_{2} ， y_{2})$ 都在函数 $y = | x | + b$ 的图像上，当 $x_{1} x_{2} > 0$ 时，若总有 $y_{1} < y_{2}$ ，结合函数图象，直接写出 $x_{1}$ 和 $x_{2}$ 的大小关系．

查看试题解析
24. 如图，在正方形ABCD中，P为边BC上一点（点P不与点B，C重合），连接DP，作点A关于直线DP的对称点E，连接AE分别交DP，DC于点G，H．过点C作 $C F ⊥ A E$ 于点F，连接DE．

(1)、依题意补全图形；

(2)、求证： $C F = E F$ ；

(3)、连接FB，FD，用等式表示线段FA，FB，FD之间的数量关系，并证明．

查看试题解析
25. 在平面直角坐标系xOy中，直线 $l ： y = k x + 4 (k \neq 0)$ 与y轴交于点A，点B和点C的坐标分别是 $(m ， y_{1})$ 和 $(m + 2 ， y_{2})$ ．

(1)、当 $y_{1} = y_{2} = 0$ 时，△ABC的面积是；

(2)、若点B和点C都在直线l上，当 $B C \leq \sqrt{5}$ 时，k的取值范围是．

查看试题解析
26. 对于定点P和图形W，给出如下定义：若图形W上存在两个不同的点M，N，使得四边形PMQN是平行四边形，则称点Q是点P关于图形W的衍生点．特别地，当平行四边形PMQN的面积最大时，称点Q是点P关于图形W的最佳衍生点．在平面直角坐标系xOy中，点 $A (0 ， 1)$ ， $B (1 ， 1)$ ， $C (0 ， 2)$ ， $D (0 ， 3)$ ， $E (\frac{3}{2} ， 2)$ ．

(1)、点C，D，E中，点O关于线段AB的衍生点是；

(2)、将点O关于线段AB的最佳衍生点记为T，
①直接写出点T的坐标；
②若直线 $y = - x + b$ 上存在点O关于四边形ABTC的衍生点，求b的取值范围．

查看试题解析

$x$	…	-3	-2	-1	0	1	2	3	…
$y = \| x \|$	…	3	2	1	0	1	2	3	…
$y = \| x \| + 1$	…	4	$m$	2	1	2	3	4	…
$y = \| x \| - 2$	…	1	0	$n$	-2	-1	0	1	…

	平均数	中位数	众数
七年级	78	79.5	79
八年级	79	$m$	75