北京市通州区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-10-21 类型:期末考试
一、单选题
-
1. 下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )A、

B、
B、
C、
C、
D、
D、
2. 一元二次方程的二次项系数、一次项系数、常数项分别是( )A、1,3,-4 B、0,3,4 C、0,-3,4 D、1,-3,-43. 在下列条件中,能判定四边形为矩形的是( )A、两组对边分别平行 B、四个内角度数相等 C、对角线长度相等 D、对角线互相垂直4. 如果 , 那么的值是( )A、0 B、2 C、0,2 D、0,-25. 某少年军校准备从甲、乙、丙三位同学中选拔一人参加全市射击比赛.在选拔比赛中,三个人10次射击成绩的统计结果如下表.
2. 一元二次方程的二次项系数、一次项系数、常数项分别是( )A、1,3,-4 B、0,3,4 C、0,-3,4 D、1,-3,-43. 在下列条件中,能判定四边形为矩形的是( )A、两组对边分别平行 B、四个内角度数相等 C、对角线长度相等 D、对角线互相垂直4. 如果 , 那么的值是( )A、0 B、2 C、0,2 D、0,-25. 某少年军校准备从甲、乙、丙三位同学中选拔一人参加全市射击比赛.在选拔比赛中,三个人10次射击成绩的统计结果如下表.同学
最高水平/环
平均数/环
中位数/环
方差
甲
10
8.3
8.5
1.5
乙
10
8.3
8.5
2.8
丙
10
8.3
8.5
3.2
经比较,推荐甲参加比赛,理由是甲的( )
A、最高水平较高 B、平均水平较高 C、成绩好的次数较多 D、射击技术稳定6. 在某游乐场,以中心广场为观测点,若有序数对表示图中“太阳神车”的位置,有序数对表示图中“雪域金翅”的位置,则与图中“天地双雄”位置对应的有序数对为( ) A、 B、 C、 D、7. 对频数分布直方图的下列认识,错误的是( )A、每小组条形图的横宽等于这组的组距 B、每小组条形图的纵高等于这组的频数 C、每小组条形图的面积等于这组的频率 D、所有小组条形图的个数等于数据分组整理的组数8. 如图,中国国家博物馆收藏了元代制作的计时工具“铜壶滴漏”,这是目前发现形制最大、最完备的一个多级滴漏,从1316年使用到1919年,一直为人民报时、计时.从上至下的四个铜壶依次名为“日壶”、“月壶”、“星壶”、“受水壶”,通过多级滴漏,使得“星壶”中的水可以匀速滴入圆柱形的“受水壶”中,“受水壶”中带有刻度的木箭随着水位匀速上移,对准标尺就能读出相应的时间.在一天中,“受水壶”中的水面高度h与时间t的函数图象可能是( )
A、 B、 C、 D、7. 对频数分布直方图的下列认识,错误的是( )A、每小组条形图的横宽等于这组的组距 B、每小组条形图的纵高等于这组的频数 C、每小组条形图的面积等于这组的频率 D、所有小组条形图的个数等于数据分组整理的组数8. 如图,中国国家博物馆收藏了元代制作的计时工具“铜壶滴漏”,这是目前发现形制最大、最完备的一个多级滴漏,从1316年使用到1919年,一直为人民报时、计时.从上至下的四个铜壶依次名为“日壶”、“月壶”、“星壶”、“受水壶”,通过多级滴漏,使得“星壶”中的水可以匀速滴入圆柱形的“受水壶”中,“受水壶”中带有刻度的木箭随着水位匀速上移,对准标尺就能读出相应的时间.在一天中,“受水壶”中的水面高度h与时间t的函数图象可能是( ) A、
A、 B、
B、 C、
C、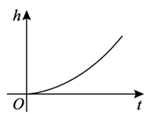 D、
D、
二、填空题
-
9. 一个多边形的内角和是720°,那么这个多边形是 边形.10. 在平面直角坐标系中有一点 , 请你写出一个一次函数表达式,使得这个一次函数的图象经过点 . 这个表达式为: .11. 关于x的方程的 有两个相等的实数根,则m的值为 .12. 若 , 是一次函数的图象上的两个点,则与的大小关系是(“>”,“=”或“<”).13. 在菱形ABCD中,两条对角线AC=8,BD=6,则此菱形的高为 .14. 某注册平台三月份新注册用户为653万,五月份新注册用户为823万,设四、五两个月新注册用户每月平均增长率为 , 则列出的方程是 .15. 寒假期间,滑雪冬令营的同学们都参加了“单板滑雪”这个项目的40次的训练测试,每次测试成绩分别为5分,4分,3分,2分,1分五档,甲、乙两位同学在这个项目的测试成绩统计结果如图所示:
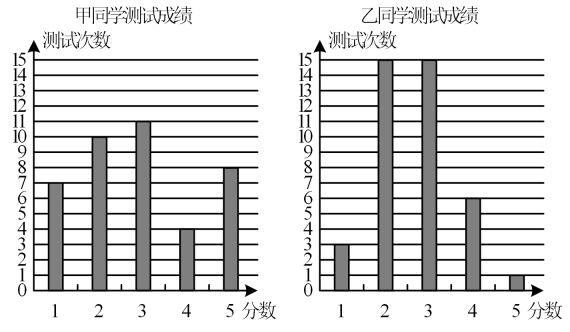
结合图中数据,请你从平均数、众数、中位数、方差中选择一方面评论一下两位同学的滑雪成绩 .
16. 如图五边形中, , . 将它放入某平面直角坐标系后,若顶点 , , , 的坐标分别是 , , , , 则点的坐标是 .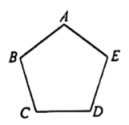
三、解答题
-
17. 解方程:18. 如图,在▱ABCD中,E,F分别在AD,BC上,且AE=CF,连结BE、DF.求证:BE=DF.
 19. 已知关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、若 为正整数,求此时方程的根.20. 已知一次函数 的图象与 轴交于点 ,与正比例函数 的图象交于点 .
19. 已知关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、若 为正整数,求此时方程的根.20. 已知一次函数 的图象与 轴交于点 ,与正比例函数 的图象交于点 .( )分别求 , 的值;
21. 已知:线段 , 以线段为对角线,求作:矩形 .
小明的作法如下.
作法:
①分别以点 , 为圆心,大于:的同样长为半径作弧,两弧分别交于点 , ;
②作直线 , 交于点;③以点为圆心,以长为半径作圆;④作圆的直径(异于直径);⑤连接 , , , 所以四边形即为所求作的知形.
(1)、请你用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明..证明:∵ ,
∴是线段的垂直平分线( )
∴点为线段的中点.
∴ , 又∵ , ∴
∴四边形是矩形( )(填推理的依据).
22. 用长为6米的铅合金条制成如图所示的矩形窗框,其中//// , 设窗框的高度为米. (1)、设窗框宽度为米,则米(用含的代数式表示);(2)、当窗户的透光面积为1.5平方米时,请你计算出窗框的高和宽分别是多少米(铝合金条的宽度忽略不计)23. 只有一组对边平行的四边形叫做梯形,平行的两条边叫做梯形的底,不平行的两条边叫做梯形的腰;两腰相等的梯形叫做等腰梯形,如图,四边形是等腰梯形,请你结合我们学习四边形的经验,猜想并证明等腰梯形的一条性质.
(1)、设窗框宽度为米,则米(用含的代数式表示);(2)、当窗户的透光面积为1.5平方米时,请你计算出窗框的高和宽分别是多少米(铝合金条的宽度忽略不计)23. 只有一组对边平行的四边形叫做梯形,平行的两条边叫做梯形的底,不平行的两条边叫做梯形的腰;两腰相等的梯形叫做等腰梯形,如图,四边形是等腰梯形,请你结合我们学习四边形的经验,猜想并证明等腰梯形的一条性质. (1)、文字描述性质;(2)、证明过程
(1)、文字描述性质;(2)、证明过程已知: ▲
求证: ▲
证明:
24. 秋季新学期开学时,某中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:分数段
频数
频率
9
36
0.4
27
0.3
0.2

请根据上述统计图表,解答下列问题:
(1)、在表中, , ;(2)、补全频数分布直方图;(3)、根据以上的数据,如果90分以上(含90分)算做优秀,该学校有七年级学生1000名,请你估算一下该学校七年级学生成绩优秀的人数.25. 如图,在中, , 点为中点.过点作 , 交射线于点 , 连接 , 点为中点,连接 , . (1)、求证:四边形是平行四边形;(2)、请你直接写出当满足什么条件时,四边形为菱形.
(1)、求证:四边形是平行四边形;(2)、请你直接写出当满足什么条件时,四边形为菱形.
