北京市房山区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-10-21 类型：期末考试

进入出卷网下载

一、单选题

1. 当 $x = 0$ 时，点 $P (x ， y)$ 一定在（）

A、x轴 B、y轴 C、坐标原点 D、第一象限

查看试题解析
2. 在如图所示的四个函数图象中，y的值随x的增大而增大的是（）

A、 B、 C、 D、

查看试题解析
3. 下面图形中既是轴对称图形又是中心对称图形的是（）

A、笛卡尔心形线 B、阿基米德螺旋线 C、科克曲线 D、赵爽弦图

查看试题解析
4. 下列几个常见统计量中能够反映一组数据变化范围大小的是（）

A、方差 B、中位数 C、众数 D、极差

查看试题解析
5. 方程 $x^{2} - x + 1 = 0$ 的根的情况是（）

A、有两个相等实数根 B、有两个不相等实数根 C、没有实数根 D、无法判断

查看试题解析
6. 如图， $▱ A B C D$ 的对角线 $A C 、 B D$ 交于点O， $△ A O B$ 是等边三角形， $A B = 2$ ，则 $▱ A B C D$ 的面积为（）

A、 $4 \sqrt{3}$ B、 $4 \sqrt{2}$ C、 $3 \sqrt{3}$ D、8

查看试题解析
7. 为庆祝中国共产主义青年团成立100周年，某区举办了团课知识竞赛，甲、乙两所中学各派5名学生参加，两队学生的竞赛成绩如图所示，下列关系完全正确的是（）

A、 $S_{甲}^{2} < S_{乙}^{2}$ ， $\bar{x_{甲}} = \bar{x_{乙}}$ B、 $S_{甲}^{2} = S_{乙}^{2}$ ， $\bar{x_{甲}} > \bar{x_{乙}}$ C、 $S_{甲}^{2} > S_{乙}^{2}$ ， $\bar{x_{甲}} = \bar{x_{乙}}$ D、 $S_{甲}^{2} = S_{乙}^{2}$ ， $\bar{x_{甲}} < \bar{x_{乙}}$

查看试题解析
8. 如图，匀速地向该容器内注水（单位时间内注水体积相同），在注满水的过程中，满足容器中水面的高度y与时间x之间函数关系的图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 函数 $y = \frac{2}{x + 3}$ 的自变量x的取值范围是．

查看试题解析
10. 方程 $x^{2} - 2 x - 3 = 0$ 的解是．

查看试题解析
11. 已知一个多边形的每一个外角都等于72°，则这个多边形的边数是.

查看试题解析
12. 关于x的一元二次方程 $(3 - m) x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则m的取值范围为．

查看试题解析
13. 特殊时期，市疾控专家提醒广大市民，乘坐电梯切莫大意，务必做好个人防护措施．如图所示，某商场在厢式电梯地面铺设了醒目的隔离带，提醒顾客乘坐电梯时持足够的空间距离，减少接触．电梯地面部分为一个长为 $190 c m$ ，宽为 $170 c m$ 的矩形地面，已知无隔离带区域（空白部分）的面积为 $29700 c m^{2}$ ，若设隔离带的宽度均为 $x c m$ ，那么x满足的一元二次方程是．

查看试题解析
14. 画一个任意四边形 $A B C D$ ，顺次连接各边中点E、F、G、H，所得到的新四边形 $E F G H$ 称为中点四边形．当原四边形 $A B C D$ 满足时，中点四边形 $E F G H$ 为菱形．

查看试题解析
15. 一次函数的图象经过点 $(2 ， - 1)$ ，且与两坐标轴围成等腰三角形，则此函数的表达式为．

查看试题解析
16. 已知：直线y=-x+1与x轴、y轴分别交于点A、点B，当点P在直线 $A B$ 上运动时，平面内存在点Q，使得以点O、P、B、Q为顶点的四边形是菱形，请你写出所有满足条件的点Q的坐标．

查看试题解析

三、解答题

17. 一次函数 $y = k x + b (k \neq 0)$ 与y轴交点纵坐标为-3，与x轴交点的横坐标为-1．

(1)、在坐标系中画出一次函数 $y = k x + b (k \neq 0)$ 的图象；

(2)、结合图象解答下列问题：
①当 $x > 0$ 时，y的取值范围是；
②当 $- 3 < y < 0$ 时，x的取值范围是；

查看试题解析
18. 解方程：

(1)、 $x^{2} = 5 x$ ；

(2)、 $2 x^{2} - 4 x + 1 = 0$ （用配方法）

查看试题解析
19. 如图， $▱ A B C D$ 中，点 $E$ 、 $F$ 分别在 $A B$ 、 $C D$ 上，且 $B E = D F$ .求证： $A F = E C$ ．

查看试题解析
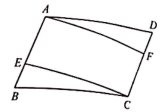20. 尺规作图：过直线外一点作已知直线的垂线．
已知：如图1所示，直线l及直线外一点P．
求作：直线l的垂线 $P C$ ．
作法：⑴如图2，在直线l上选取点A，连接 $P A$ ；
⑵以点P为圆心，线段 $P A$ 的长为半径作孤，此孤与直线l交于点B（不与点A重合）；
⑶分别以，点A、点B为圆心，以线段 $P A$ 的长为半径画孤，两弧在直线l下方交于点C；
⑷作直线 $P C$ ；
则直线 $P C$ 就是所求作的直线l的垂线．

(1)、请你根据作法用尺规将图2补全，保留作图痕迹；

(2)、补全以下证明过程：连接 $P B 、 A C 、 B C$ ，由题意可知 $P A = P B = C A = C B$ ，
∴四边形 $P A C B$ 是 ▲ 形（）
∴ $P C ⊥ A B$ （）
即直线 $P C ⊥ l$ ．

查看试题解析
21. 已知：如图， $▱ A B C D$ 中，O为对角线 $A C 、 B D$ 的交点， $B D$ 平分 $∠ A B C$ ．在 $O A$ 上截取 $O E = O D$ ，在 $O C$ 上截取 $O F = O D$ ．连结 $D E 、 E B 、 B F 、 F D$ ．

(1)、求证： $▱ A B C D$ 是菱形．

(2)、判断四边形 $B F D E$ 的形状并证明．

查看试题解析

22. 下面是证明三角形中位线定理的两种添加辅助线的方法，选择其中一种，完成证明．

已知：如图， $△ A B C$ 中，D、E分别是 $A B 、 A C$ 的中点．

求证： $D E$ ∥ $B C$ ，且 $D E = \frac{1}{2} B C$ ．

方法一

证明：如图，延长 $D E$ 至点F，使 $E F = D E$ ，连接 $C F$ ．

方法二

证明：如图，过点C作 $C F$ ∥ $A B$ 交 $D E$ 的延长线于F．

查看试题解析

23. 已知关于x的一元二次方程 $x^{2} + m x + n = 0$ ．

(1)、当 $n = m - 3$ 时，不解方程，判断方程根的情况，并说明理由．

(2)、若方程有两个相等的非零实数根，写出一组满足条件的m，n的值，并求此时方程的根．

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图象由函数 $y = x$ 的图象平移得到，且经过点(1，2)．

(1)、求这个一次函数的解析式；

(2)、当 $x > 1$ 时，对于 $x$ 的每一个值，函数 $y = m x (m \neq 0)$ 的值大于一次函数 $y = k x + b$ 的值，直接写出 $m$ 的取值范围．

查看试题解析
25. 居家学习期间，为提高学生的身体素质，某中学开展了以“运动战疫情，跳出我青春”为主题的线上跳绳比赛，同学们通过拍摄视频的方式记录下1分钟内的跳绳个数．该学校共有400名同学参加了本次活动，我们从中随机抽取了40名同学的1分钟跳绳个数作为成绩数据，并对数据进行整理、描述和分析．下面给出了部分信息．
a.40名同学1分钟跳绳成绩的频数分布表和频数分布直方图如下：
40名同学1分钟跳绳成绩的频数分布表（表1）
跳绳成绩x（个）
频数
频率
$60 \leq x < 80$
2
0.05
$80 \leq x < 100$
8
0.20
$100 \leq x < 120$
m
0.15
$120 ≤ x < 140$
8
0.20
$140 ≤ x < 160$
n
k
$160 ≤ x < 180$
6
0.15
$180 \leq x < 200$
6
0.15
合计
40
1.00
b.40名同学1分钟跳绳成绩在 $120 ≤ x < 140$ 这一组的数据如下表（表2）所示：
跳绳成绩（个）
120
125
128
135
频数
3
2
1
2
根据以上信息，回答下列问题：

(1)、表1中m的值为；k的值为．

(2)、补全该校40名学生1分钟跳绳成绩频数分布直方图．

(3)、样本数据的中位数是．

(4)、学校准备对1分钟跳绳成绩“不少于180个”以上的同学进行表彰，通过分析样本数据，估计400名参与者中可获得表彰的有名．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，函数 $y = 2 x$ 的图象与函数 $y = - k x + 3$ 的图象交于点 $A (1 ， m)$ ．

(1)、求k的值；

(2)、过点A作x轴的平行线l，直线 $y = 2 x + b$ 与直线l交于点B，与函数 $y = - k x + 3$ 的图象交于点C，与x轴交于点D．当点 $B D = 2 B C$ 时，求b的值．

查看试题解析
27. 矩形 $A B C D$ 中，点M是对角线 $B D$ 上的一个动点（点M不与点B，D重合），分别过点B，D向射线 $A M$ 作垂线，垂足分别为点E，F，点O为 $B D$ 的中点．

(1)、如图1，当点M与点O重合时，请你判断 $O E$ 与 $O F$ 的数量关系，并加以证明；

(2)、当点M运动到如图2所示位置时，请你在图2中补全图形，判断（1）中的结论是否仍然成立，并加以证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于A，B两点给出如下定义：若点A到x、y轴的距离中的最大值等于点B到x、y轴的距离中的最大值，则称A，B两点为“同值点”．
例如，图中的A，B两点即为“同值点”．

(1)、已知点P的坐标为 $(- 2 ， 3)$ ，
①在点 $C (3 ， - 5) ， D (0 ， 2) ， E (- 3 ， 1)$ 中，是点P的“同值点”的有；
②若点Q在直线 $y = x - 5$ 上，且P，Q两点为“同值点”，则点Q的坐标为；

(2)、若 $M_{1} (- 1 ， m_{1}) ， M_{2} (2 ， m_{2})$ 是直线 $l ： y = k x + 1 (k < 0)$ 上的两点，且 $M_{1}$ 与 $M_{2}$ 为“同值点”，求k的值．

查看试题解析

跳绳成绩x（个）	频数	频率
$60 \leq x < 80$	2	0.05
$80 \leq x < 100$	8	0.20
$100 \leq x < 120$	m	0.15
$120 ≤ x < 140$	8	0.20
$140 ≤ x < 160$	n	k
$160 ≤ x < 180$	6	0.15
$180 \leq x < 200$	6	0.15
合计	40	1.00

跳绳成绩（个）	120	125	128	135
频数	3	2	1	2