北京市朝阳区2021-2022年八年级下学期期末数学试题
试卷更新日期:2022-10-21 类型:期末考试
一、单选题
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 以下列各组数为边长的线段,可以组成直角三角形的是( )A、2,2,3 B、4,5,7 C、5,12,13 D、10,10,103. 下列各曲线中,不表示y是x的函数的是( )A、
 B、
B、 C、
C、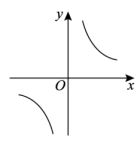 D、
D、 4. 如图,在平面直角坐标系xOy中, , B(0,3),P为线段AB的中点,则线段OP的长为( )
4. 如图,在平面直角坐标系xOy中, , B(0,3),P为线段AB的中点,则线段OP的长为( ) A、 B、2 C、 D、55. 某农民统计了自己养鸡场1000只鸡出售时质量的数据,如下表:
A、 B、2 C、 D、55. 某农民统计了自己养鸡场1000只鸡出售时质量的数据,如下表:质量/kg
1.0
1.2
1.5
1.8
2.0
频数
108
226
325
245
96
这组数据的众数是( )
A、1.0 B、1.5 C、1.8 D、2.06. 若是整数,则正整数n的最小值是( )A、3 B、7 C、9 D、637. 小明同学在一次学科综合实践活动中发现,某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系,下表给出y与x的一些对应值:码数x
26
30
34
42
长度y cm
18
20
22
26
根据小明的数据,可以得出该品牌38码鞋子的长度为( )
A、24cm B、25cm C、26cm D、38cm8. 如图,在甲、乙两个大小不同的6×6的正方形网格中,正方形ABCD,EFGH分别在两个网格上,且各顶点均在网格线的交点上.若正方形ABCD,EFGH的面积相等,甲、乙两个正方形网格的面积分别记为 , , 有如下三个结论:①正方形ABCD的面积等于的一半;②正方形EFGH的面积等于的一半;③ .

上述结论中,所有正确结论的序号是( )
A、①② B、②③ C、③ D、①②③二、填空题
-
9. 计算: .10. 若 在实数范围内有意义,则实数x的取值范围是 .11. 如图,数轴上点P表示的实数是 .
 12. 如图,在中,AE⊥BC于点E,点F在BC边的延长线上,只需再添加一个条件即可证明四边形AEFD是矩形,这个条件可以是(写出一个即可).
12. 如图,在中,AE⊥BC于点E,点F在BC边的延长线上,只需再添加一个条件即可证明四边形AEFD是矩形,这个条件可以是(写出一个即可). 13. 如图,在平面直角坐标系xOy中,四边形OBCD是正方形,点B(1,0),请写出一个图象与该正方形有公共点的函数表达式: .
13. 如图,在平面直角坐标系xOy中,四边形OBCD是正方形,点B(1,0),请写出一个图象与该正方形有公共点的函数表达式: . 14. 某市2021年和2022年5月1日至5日每日最高气温(单位:℃)如下表:
14. 某市2021年和2022年5月1日至5日每日最高气温(单位:℃)如下表:1日
2日
3日
4日
5日
2021年
22
22
24
24
25
2022年
27
26
31
33
30
则这五天的最高气温更稳定的是年(填“2021”或“2022”).
15. 我国古代用天干和地支纪年,其中天干有10个:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;地支有12个:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.将天干的10个汉字和地支的12个汉字分别循环排列成如下两行:甲 乙 丙 丁 戊 己 庚 辛 壬 癸 甲 乙 丙 丁 戊 己 庚 辛 壬 癸……
子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥 子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥……
从左向右第1列是甲子,可以表示甲子年,第4列是丁卯,可以表示丁卯年……
(1)、在上面的天干排列中,丙第n(n是正整数)次出现,位于从左向右的第列(用含n的式子表示);(2)、2022年是壬寅年,表示该年的壬寅可以位于从左向右的第列(写出一个即可).三、解答题
-
16. 已知直线l及线段AB,点B在直线上,点A在直线外.如图,

⑴在直线l上取一点C(不与点B重合),连接AC;
⑵以点A为圆心,BC长为半径作弧,以点B为圆心,AC长为半径作弧,两弧交于点D(与点C位于直线AB异侧);
⑶连接CD交AB于点O,连接AD,BD.
根据以上作图过程及所作图形,在下列结论①OA=OB;②;③∠ACD=∠ADC中,一定正确的是(填写序号).
17. 计算: .18. 如图,在中,E,F分别是AB,CD的中点,求证:AF=CE. 19. 已知 , , 求代数式的值.20. 如图,在四边形ABCD中,BC=CD,∠ADB=∠C=90°,∠A=60°, . 求CD的长.
19. 已知 , , 求代数式的值.20. 如图,在四边形ABCD中,BC=CD,∠ADB=∠C=90°,∠A=60°, . 求CD的长. 21. 已知一次函数与的图象都经过点(2,1).
21. 已知一次函数与的图象都经过点(2,1). (1)、求k,b的值;(2)、在同一直角坐标系中画出这两个一次函数的图象,并结合函数图象,直接写出当x取何值时, .22. 如图,在△ABC中,AB=AC,D,E分别是AB,BC的中点, , .
(1)、求k,b的值;(2)、在同一直角坐标系中画出这两个一次函数的图象,并结合函数图象,直接写出当x取何值时, .22. 如图,在△ABC中,AB=AC,D,E分别是AB,BC的中点, , . (1)、求证:四边形BDEF是菱形;(2)、连接DF交BC于点M,连接CD,若BE=4, , 求DM,CD的长.23. 为了解我国2022年25个地区第一季度快递业务收入情况,收集了这25个地区第一季度快递业务收入(单位:亿元)的数据,并对数据进行了整理、描述和分析,给出如下信息.
(1)、求证:四边形BDEF是菱形;(2)、连接DF交BC于点M,连接CD,若BE=4, , 求DM,CD的长.23. 为了解我国2022年25个地区第一季度快递业务收入情况,收集了这25个地区第一季度快递业务收入(单位:亿元)的数据,并对数据进行了整理、描述和分析,给出如下信息.
a.排在前5位的地区第一季度快递业务收入的数据分别为:
534.9 437.0 270.3 187.7 104.0
b.其余20个地区第一季度快递业务收入的数据的频数分布表如下:
c.第一季度快递业务收入的数据在20≤x<40这一组的是:快递业务收入x 0≤x<20 20≤x<40 40≤x<60 60≤x≤80 频数 6 10 1 3
20.2 20.4 22.4 24.2 26.1 26.5 28.5 34.4 39.1 39.8d.排在前5位的地区、其余20个地区、全部25个地区第一季度快递业务收入的数据的平均数、中位数如下:
前5位的地区
其余20个地区
全部25个地区
平均数
306.8
29.9
n
中位数
270.3
m
28.5
根据以上信息,回答下列问题:
(1)、表中m的值为;(2)、在下面3个数中,与表中n的值最接近的是(填写序号);①30 ②85 ③150
(3)、根据(2)中的数据,预计这25个地区2022年全年快递业务收入约为亿元.24. 在平面直角坐标系xOy中,直线与x轴交于点A,与y轴交于点B.(1)、求点A,B的坐标;(2)、点A关于y轴的对称点为C,将直线、直线BC都沿y轴向上平移t()个单位,点在直线平移后的图形上,点在直线BC平移后的图形上,试比较m,n的大小,并说明理由.25. 点E在正方形ABCD的AD边上(不与点A,D重合),点D关于直线CE的对称点为F,作射线DF交CE于点M,连接BF. (1)、求证:;(2)、过点A作交射线DF于点H.
(1)、求证:;(2)、过点A作交射线DF于点H.①求∠HFB的度数;
②用等式表示线段AH与DF之间的数量关系,并证明.
26. 对于平面直角坐标系xOy中的直线l:与矩形OABC给出如下定义:设直线l与坐标轴交于点M,N(M,N不重合),直线与矩形OABC的两边交于点P,Q(P,Q不重合),称线段MN,PQ的较小值为直线l的关联距离,记作 , 特别地,当MN=PQ时, .
已知A(6,0),B(6,3),C(0,3).
(1)、若 , 则MN= , PQ=;(2)、若 , , 则b的值为;(3)、若 , 直接写出的最大值及此时以M,N,P,Q为顶点的四边形的对角线交点坐标.