北京市昌平区2021-2022学年八年级下学期期末数学试题
试卷更新日期：2022-10-21 类型：期末考试
一、单选题
-
1. 一个多边形的内角和与外角和相等，这个多边形是（ ）A、三角形 B、四边形 C、五边形 D、六边形2. 函数中，自变量x的取值范围是（ ）A、 B、 C、 D、3. 全球新能源汽车发展已进入不可逆的快车道，中国的新能源汽车产业一直在增长，不断迈上新台阶．下列图形是我国国产部分新能源品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（ ）A、
B、
C、
D、
4. 下列各曲线中，表示y是x的函数的是（ ）A、
B、
C、
D、
5. 下列图形中，具备“对角线相等”的性质的是（ ）A、平行四边形 B、菱形 C、梯形 D、矩形6. 用配方法解一元二次方程 ， 配方后得到的方程是（ ）A、 B、 C、 D、7. 如图，是的中位线，的角平分线交于点 ， ， ， 则的长为（ ）
A、1 B、1.5 C、2 D、2.58. 在物理实验课上，小鹏利用滑轮组及相关器材进行实验，他把得到的拉力和所悬挂物体的重力的几组数据用电脑绘制成如下图象（不计绳重和摩擦），请你根据图象判断以下结论正确的序号有（ ）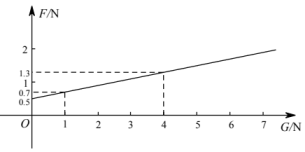
①物体的拉力随着重力的增加而增大；②当物体的重力N时，拉力N；③拉力F与重力G成正比例函数关系；④当滑轮组不悬挂物体时，所用拉力为0.5N．
A、①② B、②④ C、①④ D、③④二、填空题
-
9. 如果点在第一象限，则m的取值范围是 ．10. 体育课上，小明和小亮练习掷实心球，下面是两人7次练习成绩的折线统计图，则这两人中掷实心球成绩较稳定的是 ． （填“小明”或“小亮”）
11. 我们在生活中经常见到如图所示的电动伸缩门，它能伸缩是利用了四边形的 ．
12. 把直线向上平移3个单位长度后的直线表达式为 ．13. 如图，在△ABC中，∠ACB＝90°，点D为AB的中点，连接DC，若BC＝3，AC＝4，则△BDC的周长为 ．
14. 如图，把正方形纸片ABCD沿对边中点所在的直线对折后展开，折痕为MN，再过点B折叠纸片，使点A落在MN上的点F处，折痕为BE．若FN＝3，则正方形纸片的边长为 ．
15. 2022年女足亚洲杯在2022年1月20日至2月6日举行，由小组赛和淘汰赛组成．按比赛规则小组赛赛制为单循环赛制（即每个小组的两个球队之间进行一场比赛），在小组赛阶段，中国队凭借着小组赛比赛前几个场次的赢球，成为最先获得八强资格的球队，并在2022年2月6日的亚洲杯决赛中以3∶2战胜韩国女足，获得亚洲杯冠军．已知中国女足队所在的A组共安排了6场比赛，则中国女足所在的A组共有支球队．16. 在平面直角坐标系xOy中，已知的顶点在第二象限，点O为AC的中点，边轴，当AB＝1时，点D的坐标为 ．三、解答题
-
17. 解方程： ．18. 已知：如图，在 中， 是对角线 上两个点，且 ．求证：
19. 在平面直角坐标系xOy中，一次函数的图象经过点 ， ， 且与x轴相交于点C．(1)、求k，b的值；(2)、求 ．20. 某印刷厂一月份印了50万册书，三月份印了60.5万册，那么这个印刷厂印数的月平均增长率是多少？21. 在数学课上，老师提出问题：如何用尺规作一个矩形？小华的设计如下：
①如图，任取一点O，过点O作直线 ， ；
②以O为圆心，任意长为半径作圆，与直线交于点A，C，与直线交于点B，D；
③连接AB，BC，CD，DA．
所以，四边形ABCD即为所求作的矩形．
老师说小华的设计是正确的，请你根据小华的设计完成以下问题：
(1)、在作图区内，使用直尺和圆规，补全图形（保留作图痕迹）；(2)、将证明四边形ABCD是矩形的过程书写完整．22. 为了保护视力，学校开展了全校性的视力保健活动（视力达到4.8及以上为达标），活动前随机抽取部分学生，检查他们的视力，结果如图所示（数据包括左端点不包括右端点，精确到0.1）．活动后再次检查这部分学生的视力，结果如表所示．
抽取的学生活动后视力频数分布表
分组
频数
2
3
5
a
15
5
(1)、若活动后所抽取学生的视力达标率为50%，求a的值；(2)、补全频数分布直方图；(3)、分析活动前后相关数据，对视力保健活动的效果进行评价．23. 已知关于x的一元二次方程 ．(1)、求证：无论m为何值，方程总有两个实数根；(2)、若方程只有一个根为负数，求m的取值范围．24. 昌平区公共自行车智能系统，是响应国家“低碳环保，绿色出行”号召，基于“服务民生”理念，运用信息化管理与服务手段，自2016年底开始为居住区、旅游景点等人流量集中地区提供充费公共自行车服务的智能交通系统．对于优化城市交通状况、解决“交通末端”难题及改善城市居住环境都有重要意义．据小丽调查了解，为充分发挥市场机制配置优势，进一步优化社会资源配给，为居民提供更便捷的服务，昌平区公共自行车实施新的运营模式：自2021年4月1日起，收费标准变更为1元/30分钟（不足30分钟按30分钟计算），超过30分钟按0.5元/15分钟依次累加（不足15分钟按15分钟计算）．
设使用自行车的时间为x分钟，费用为y元．
(1)、若 ， 则使用费用元；(2)、若使用时间（x为15的整倍数），求y与x之间的函数关系式；(3)、若小丽此次使用公共自行车付费2元，请说明她所使用的时间范围．25. 如图，在中，延长BC到点E使CE＝BC，连接AC，DE．
(1)、求证：四边形ACED是平行四边形；(2)、连接AE交DC于点F．①当∠AFC为°时，四边形ACED是菱形；
②若∠B＝70°，则当∠AFC为°时，四边形ACED是矩形．
26. 在平面直角坐标系xOy中，一次函数的图像过点 ， ， 点B关于x轴的对称点为C．
(1)、求这个一次函数的表达式；(2)、点D为x轴上任意一点，求线段AD与线段CD之和的最小值；(3)、一次函数）的图像经过点C，当时，对于x的每一个值，的值都小于的值，直接写出a的取值范围．27. 在菱形ABCD中，∠BCD＝60°，点P是直线AB上一点，且不与点A，点B重合，连接CP，作等边三角形PCE．
(1)、如图1，若点P在线段AB上，连接DE，则线段PB，DE之间的数量关系是；(2)、如图2，若点P在线段AB的延长线上，连接AE，求证：EA＝EP；(3)、如图3，若点P在线段BA的延长线上，顺次连接四边形ABCE各边的中点，则所得四边形的形状是 ．28. 定义：对于平面直角坐标系xOy中的两个图形M，N，图形M上的任意一点与图形N上的任意一点的距离中的最小值，叫做图形M与图形N的距离．若图形M与图形N的距离小于等于1，称这两个图形互为“近邻图形”．
(1)、已知点 ， 点 ．①如图1，在点 ， ， 中，与线段AB互为“近邻图形”的是 ▲ ；
②如图2，将线段AB向下平移2个单位，得到线段DC，连接AD，BC，若直线与四边形ABCD互为“近邻图形”，求b的取值范围；
(2)、如图3，在正方形EFGH中，已知点 ， 点 ， 若点与正方形EFGH互为“近邻图形”，直接写出m的取值范围．