安徽省滁州市定远县永康片2021-2022学年八年级下学期期末考试数学试题

试卷更新日期：2022-10-21 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{a + 1}$ 在实数范围内有意义，则a的取值范围是（）

A、 $a \geq 1$ B、 $a \geq - 1$ C、 $a > 1$ D、 $a \leq - 1$

查看试题解析
2. 计算 $(\sqrt{3} - 1) (\sqrt{3} + 1)^{2}$ 的结果是（）

A、 $2 \sqrt{3} + 2$ B、 $2 \sqrt{3} - 2$ C、2 D、 $\sqrt{3} + 1$

查看试题解析
3. 如果关于 $x$ 的方程 $(x - 9)^{2} = m + 4$ 可以用直接开平方法求解，那么 $m$ 的取值范围是（）

A、 $m > 3$ B、 $m \geq 3$ C、 $m > - 4$ D、 $m \geq - 4$

查看试题解析
4. 若关于x的方程x²+6x+c=0有两个相等的实数根，则c的值是（）

A、36 B、-36 C、9 D、-9

查看试题解析
5. 已知三角形的边长分别是5、7、8，则这个三角形的面积是（）

A、9 B、 $9 \sqrt{3}$ C、10 D、 $10 \sqrt{3}$

查看试题解析
6. 在 $△ A B C$ 中，若 $A B = 3 ， B C = 5 ， A C = \sqrt{34}$ ，则下列说法正确的是（）

A、 $△ A B C$ 是锐角三角形 B、 $△ A B C$ 是直角三角形且 $∠ C = 90 °$ C、 $△ A B C$ 是钝角三角形 D、 $△ A B C$ 是直角三角形且 $∠ B = 90 °$

查看试题解析
7. 如图所示，将正六边形与正五边形按此方式摆放，正六边形与正五边形的公共顶点为O，且正六边形的边AB与正五边形的边DE共线，则∠COF的度数是（）

A、86° B、84° C、76° D、74°

查看试题解析
8. 如图，平行四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O，点E是 $A D$ 中点．若 $O A = 2 ， △ A O E$ 的周长为10，则平行四边形 $A B C D$ 的周长为（）

A、16 B、32 C、36 D、40

查看试题解析
9. 如图，点E是 $△ A B C$ 内一点， $∠ A E B = 90 °$ ，D是边 $A B$ 的中点，延长线段 $D E$ 交边 $B C$ 于点F，点F是边 $B C$ 的中点，若 $A B = 6$ ， $E F = 1$ ，则线段 $A C$ 的长为（　　）

A、8 B、 $\frac{15}{2}$ C、7 D、9

查看试题解析
10. 某社区计划组织以“全民健身，‘毽’步如飞”为主题的踢毽子比赛活动，为了了解参赛成员踢毽子水平及稳定程度，在比赛前期甲、乙、丙、丁四名参赛成员分别记录了自己在规定时间内 5 次踢毽子的数量，并计算出了各自的平均个数 $\bar{x}$ 及方差S² ，如下表所示：

甲
乙
丙
丁
$\bar{x}$
90
103
95
108
S²
$\frac{26}{5}$
$\frac{18}{5}$
12
$\frac{18}{5}$
根据参赛成员踢毽子的平均数量及稳定程度，你认为哪位参赛成员获胜的可能性大（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题

11. 观察下列各式： $\sqrt{1 - \frac{1}{2}} = \sqrt{\frac{1}{2}}$ ， $\sqrt{2 - \frac{2}{5}} = 2 \sqrt{\frac{2}{5}}$ ， $\sqrt{3 - \frac{3}{10}} = 3 \sqrt{\frac{3}{10}}$ ， $\sqrt{4 - \frac{4}{17}} = 4 \sqrt{\frac{4}{17}}$ ，请你将猜想到的规律用含自然数 $n (n \geq 1)$ 的等式表示出来是．

查看试题解析
12. 已知关于x的方程 $x^{2} + 4 x + n = 0$ 可以配方成 ${(x + m)}^{2} = 3$ ，则 ${(m - n)}^{2} =$

查看试题解析
13. 如图，四边形ABCD中，AD∥BC，∠D＝90°，M是AB的中点，若CM＝6.5，BC+CD+DA＝17，则四边形ABCD的面积为．

查看试题解析
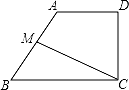14. 如图，在长方形纸片ABCD中，AB＝6，AD＝18，折叠纸片ABCD，使顶点C落在边AD上的点G处，折痕分别交边AD、BC于点E，F，则△GEF的面积最大值是．

查看试题解析

三、解答题

15. 计算：

(1)、 $\sqrt{32} - \sqrt{18} - \sqrt{\frac{1}{8}}$ ；

(2)、 $(7 + 4 \sqrt{3}) (7 - 4 \sqrt{3}) - (\sqrt{3} - 1)^{2}$ ．

查看试题解析
16. 解方程： $2 (x - 3) = x (3 - x)$ ．

查看试题解析
17.

(1)、初步感知，在④的横线上直接写出计算结果：
① $\sqrt{1^{3}} = 1$ ；② $\sqrt{1^{3} + 2^{3}} = 3$ ；③ $\sqrt{1^{3} + 2^{3} + 3^{3}} = 6$ ；④ $\sqrt{1^{3} + 2^{3} + 3^{3} + 4^{3}} =$ ；…

(2)、深入探究，观察下列等式：
① $1 + 2 = \frac{(1 + 2) \times 2}{2}$ ；② $1 + 2 + 3 = \frac{(1 + 3) \times 3}{2}$ ；③ $1 + 2 + 3 + 4 = \frac{(1 + 4) \times 4}{2}$ ；…
根据以上等式的规律，在下列横线上填写适当内容：
$1 + 2 + 3 + ⋯ + n + (n + 1) =$ ．

(3)、拓展应用，通过以上初步感知与深入探究，计算：
① $\sqrt{1^{3} + 2^{3} + 3^{3} + \dots + 9 9^{3} + 10 0^{3}}$ ；
② $1 1^{3} + 1 2^{3} + 1 3^{3} + \dots + 1 9^{3} + 2 0^{3}$ ．

查看试题解析
18. 综合与探究：如果关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有两个实数根，且其中一个根比另一个根大1，那么称这样的方程是“邻根方程”．例如：一元二次方程 $x^{2} + x = 0$ 的两个根是 $x_{1} = 0$ ， $x_{2} = - 1$ ，则方程： $x^{2} + x = 0$ 是“邻根方程”．

(1)、通过计算，判断下列方程是否是“邻根方程”：
① $x^{2} + x - 6 = 0$ ；② $2 x^{2} - 2 \sqrt{5} x + 2 = 0$ ．

(2)、已知关于x的一元二次方程 $x^{2} - (m - 2) x - 2 m = 0$ （m是常数）是“邻根方程”，求m的值．

查看试题解析
19. 如图，在等腰Rt△ABC中，∠ACB＝90°，点D是AB上一点，作等腰Rt△DCE，且∠DCE＝90°，连接AE．

(1)、求证：△CEA≌△CDB；

(2)、求证：AE²+AD²＝DE² ．

查看试题解析
20. 王老师从本校九年级质量检测中随机抽取另一些同学的数学成绩做质量分析，他先按照等级绘制这些人数学成绩的扇形统计图，如图（1）所示，数学成绩等级标准见表1；又按分数段绘制成绩分布表，如表2．

表1：

等级

A

B

C

D

分数x的范围

a≤x≤100

80≤x＜a

60≤x＜80

0≤x＜60

表2：

分数段

x＜60

60≤x＜70

70≤x＜80

80≤x＜90

90≤x≤100

人数

5

10

m

12

11

分数段为90≤x≤100的11人中，其成绩的中位数是95人份．请根据以上信息回答下面问题：

(1)、王老师抽查了人；m的值是；

(2)、小明在此考试中也正好得了95分，他说自己在这次考试中数学成绩是A等级，他说的对吗？为什么？

(3)、若此次测试数学学科普高的预测线是70分，该校九年级有900名学生，求数学学科达到普高预测线的学生约有多少人？

查看试题解析
21. 如图：

(1)、如图（1）所示，已知△OAC为等腰直角三角形 $O A = O C$ ， $∠ A O C = 90 °$ ，以点D为坐标图点建立坐标平面，作 $C H ⊥ x$ 轴于H点，求证：
① $∠ A O x = ∠ O C H$
②若点A坐标为 $(3 ， 4)$ ，求出点C的坐标．

(2)、如图（2）所示，已知△OAB，以点O为原点建立平面直角坐标系，若点A坐标为 $(3 ， 4)$ ，点B的坐标为 $(- 1 ， 7)$ ，求证：△OAB是等腰直角三角形．

(3)、如图（3）所示，在平面直角坐标系中，O是坐标原点，点A的坐标为 $(3 ， 4)$ ，若△OAB是以OA为腰的等腰直角三角形，请直接写出点B的坐标．

查看试题解析
22. 如图，在▱ABCD中，点E在边AD上，连接EB并延长至F，使BF＝BE；连接EC并延长至G，使CG＝CE，连接FG，点H为FG的中点，连接DH，AF．

(1)、若∠BAE＝70°，∠DCE＝20°，求∠DEC的度数；

(2)、求证：四边形AFHD为平行四边形．

查看试题解析
23. 如图，△ABC中，AB＝AC，∠BAC＝120°．点D是边BC上一点，△BDE是等边三角形，四边形CDEF是平行四边形．

(1)、如图1，若点D是BC中点，求证：四边形BDFE是菱形；

(2)、一般的，设DF与CE相交于点G，如图2，连接AD，AC，AF．
①证明：AD＝AF；
②求∠DAG的大小．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	90	103	95	108
S²	$\frac{26}{5}$	$\frac{18}{5}$	12	$\frac{18}{5}$

等级	A	B	C	D
分数x的范围	a≤x≤100	80≤x＜a	60≤x＜80	0≤x＜60

分数段	x＜60	60≤x＜70	70≤x＜80	80≤x＜90	90≤x≤100
人数	5	10	m	12	11