云南省玉溪市2021-2022学年高一上学期数学期末教学质量检测试卷
试卷更新日期:2022-10-21 类型:期末考试
一、单选题
-
1. 已知集合 , 集合 , 则( )A、 B、 C、 D、2. 在半径为2的圆上,一扇形的弧所对的圆心角为 , 则该扇形的面积为( )A、 B、 C、 D、3. 函数的零点所在的区间为( )A、 B、 C、 D、4. 已知角的终边过点 , 则( )A、 B、 C、 D、5. 幂函数的图象关于轴对称,且在上是增函数,则的值为( )A、 B、 C、 D、和6. 函数 , , 则函数的图象大致是( )A、
 B、
B、 C、
C、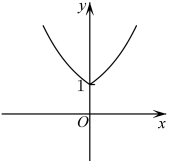 D、
D、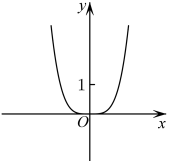 7. 已知 , , , 则a,b,c的大小关系为( )A、 B、 C、 D、8. 已知函数是定义域为的奇函数,且 , 当时, , 则( )A、 B、 C、 D、
7. 已知 , , , 则a,b,c的大小关系为( )A、 B、 C、 D、8. 已知函数是定义域为的奇函数,且 , 当时, , 则( )A、 B、 C、 D、二、多选题
-
9. 可以作为的一个充分不必要条件是( )A、 B、 C、 D、10. 已知且 , , 则下列结论一定成立的是( )A、 B、 , C、 D、11. 下列选项中,在为增函数的是( )A、 B、 C、 D、12. 已知 , , 则下列结论正确的是( )A、 B、 C、 D、
三、填空题
-
13. 函数(且)的定义域为 .14. 若正数x,y满足 , 则的最小值是 .15. 的值等于 .16. 已知函数(且),若对 , , 都有 . 则实数a的取值范围是 .
四、解答题
-
17. 求解下列问题(1)、化简(其中各字母均为正数):;(2)、化简并求值: .18. 已知集合 , .(1)、若 , 求;(2)、在① , ② , ③ , 这三个条件中任选一个作为已知条件,求实数的取值范围.19. 已知函数 .
 (1)、求的最小正周期和对称中心;(2)、填上面表格并用“五点法”画出在一个周期内的图象.20. 设关于x的二次函数 .(1)、若 , 解不等式;(2)、若不等式在上恒成立,求实数m的取值范围.
(1)、求的最小正周期和对称中心;(2)、填上面表格并用“五点法”画出在一个周期内的图象.20. 设关于x的二次函数 .(1)、若 , 解不等式;(2)、若不等式在上恒成立,求实数m的取值范围.