江西省九江市湖口县2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-10-21 类型:期中考试
一、单选题
-
1. 下列四个数中,属于无理数的是( )A、0 B、 C、-0.3 D、2. 下列各数中,是勾股数的是( )A、1, , B、16,12,20 C、12,13,7 D、0.3,0.4,0.53. 如图为小明的答卷,他的得分应是( )
计算(每小题20分,共100分)
① ② ③
④ ⑤
A、40 B、60 C、80 D、1004. 在平面直角坐标系中,点在( )A、第二象限 B、第四象限 C、x轴上 D、无法判定象限位置5. 估计的值应在( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间6. 已知中,y随x的增大而减小,则直线在直角坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、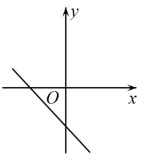 7. 如图,在中,平分交于点E,平分 , , 交于点M,若 , 则( )
7. 如图,在中,平分交于点E,平分 , , 交于点M,若 , 则( )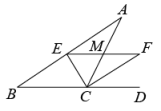 A、75 B、100 C、120 D、1258. A、B两地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶,货车两小时可到达途中C站,客车需9小时到达C站,货车的速度是客车的 , 客、货车到C站的距离分别为、千米),它们与行驶时间x(小时)之间的函数关系如图.下列说法:①客、货两车的速度分别为60千米/小时,45千米/小时;②A、C两站间的距离是540千米;③P点横坐标为12;④E点坐标为 , 其中正确的说法个数有( )
A、75 B、100 C、120 D、1258. A、B两地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶,货车两小时可到达途中C站,客车需9小时到达C站,货车的速度是客车的 , 客、货车到C站的距离分别为、千米),它们与行驶时间x(小时)之间的函数关系如图.下列说法:①客、货两车的速度分别为60千米/小时,45千米/小时;②A、C两站间的距离是540千米;③P点横坐标为12;④E点坐标为 , 其中正确的说法个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
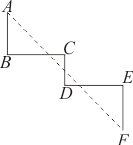
9. 的立方根是 .10. 若点在直线上,则 .11. 若点与关于y轴对称,则 .12. 在 中,斜边 ,则 .13. 若是正比例函数,则 .14. 如图,线段CE的长为4,延长EC到B,以CB为一边作正方形ABCD,连接DE,以DE为一边作正方形DEFG,设正方形ABCD的面积为S1 , 正方形DEFG的面积为S2 , 则S2﹣S1的值为 .
 15. 如图,∠AOB=45°,角内有点P,PO=10,在角的两边上有两点Q,R(均不同于O点),则△PQR的周长的最小值为 .
15. 如图,∠AOB=45°,角内有点P,PO=10,在角的两边上有两点Q,R(均不同于O点),则△PQR的周长的最小值为 . 16. 已知直线与两坐标轴所围成的三角形的面积为4,则m的值为 .
16. 已知直线与两坐标轴所围成的三角形的面积为4,则m的值为 .三、解答题
-
17. 计算:18. 先化简,再求值: , 其中 .19. 如图,已知 , 且 , , , 求A、F两点间的距离.
 20. 如图,在边长为1个单位长度的小正方形组成的网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.
20. 如图,在边长为1个单位长度的小正方形组成的网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.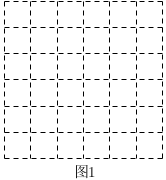
 (1)、在图1中,画一个正方形,使它的面积为10;(2)、在图2中,画一个三角形 , 使它的三边长分别为 , , ;(3)、请写出图2中所画的面积为 . (直接写出结果)21. 一个正方形的面积是13,若它的边长的整数部分是a,小数部分是b,求的值.22. 已知点M( , ),分别根据下列条件求出点M的坐标.(1)、点N的坐标是(1,6),并且直线MN//y轴;(2)、点M到两坐标轴的距离相等.23. 如图,在Rt ABC中,∠ACB=90°,AB=20cm,AC=16cm,点P从点A出发,以每秒1cm的速度向点C运动,到C点停止.连接PB,设运动时间为t秒(t>0).
(1)、在图1中,画一个正方形,使它的面积为10;(2)、在图2中,画一个三角形 , 使它的三边长分别为 , , ;(3)、请写出图2中所画的面积为 . (直接写出结果)21. 一个正方形的面积是13,若它的边长的整数部分是a,小数部分是b,求的值.22. 已知点M( , ),分别根据下列条件求出点M的坐标.(1)、点N的坐标是(1,6),并且直线MN//y轴;(2)、点M到两坐标轴的距离相等.23. 如图,在Rt ABC中,∠ACB=90°,AB=20cm,AC=16cm,点P从点A出发,以每秒1cm的速度向点C运动,到C点停止.连接PB,设运动时间为t秒(t>0). (1)、求 ABC的面积;(2)、当PA=PB时,求t的值.24. 已知一次函数的图象经过点和点 , 且点B在正比例函数的图象上.(1)、求a,b的值;(2)、求一次函数的解析式;(3)、若 , 是一次函数图象上的两点,试比较 , 的大小.25. 如图,在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为(0,6)、(-8,0)、(-3,0), , 将沿着射线AC翻折,点B落到y轴上点D处.
(1)、求 ABC的面积;(2)、当PA=PB时,求t的值.24. 已知一次函数的图象经过点和点 , 且点B在正比例函数的图象上.(1)、求a,b的值;(2)、求一次函数的解析式;(3)、若 , 是一次函数图象上的两点,试比较 , 的大小.25. 如图,在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为(0,6)、(-8,0)、(-3,0), , 将沿着射线AC翻折,点B落到y轴上点D处. (1)、求点D的坐标;(2)、动点P以每秒1个单位长度的速度从点B出发沿着线段BO向终点O运动,运动时间为t秒,请用含有t的式子表示的面积,并直接写出t的取值范围;(3)、在(2)的条件下,动点M以每秒2个单位长度的速度从点A出发沿着线段AO向终点O运动,动点N以每秒a个单位长度的速度从点O出发沿着x轴正方向运动,点P、M、N同时出发,点M停止时,点P、N也停止运动,当时,求a的值.
(1)、求点D的坐标;(2)、动点P以每秒1个单位长度的速度从点B出发沿着线段BO向终点O运动,运动时间为t秒,请用含有t的式子表示的面积,并直接写出t的取值范围;(3)、在(2)的条件下,动点M以每秒2个单位长度的速度从点A出发沿着线段AO向终点O运动,动点N以每秒a个单位长度的速度从点O出发沿着x轴正方向运动,点P、M、N同时出发,点M停止时,点P、N也停止运动,当时,求a的值.