内蒙古自治区赤峰市红山区2021-2022学年高一上学期数学期末试试卷

试卷更新日期：2022-10-21 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {1 ， 2 ， 3 ， 5 ， 7 ， 11}$ ， $B = {x | 3 < x < 15}$ ，则A∩B中元素的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 下列函数中与 $y = x$ 是同一函数的是（）
⑴ $y = \sqrt{x^{2}}$ ⑵ $y = l o g_{a} a^{x}$ ⑶ $y = a^{l o g_{a} a^{x}}$ ⑷ $y = \sqrt[3]{x^{3}}$ ⑸ $y = \sqrt[n]{x^{n}} (n \in N^{+})$

A、（1）（2） B、（2）（3） C、（2）（4） D、（3）（5）

查看试题解析
3. 某国近日开展了大规模COVID-19核酸检测，并将数据整理如图所示，其中集合S表示（）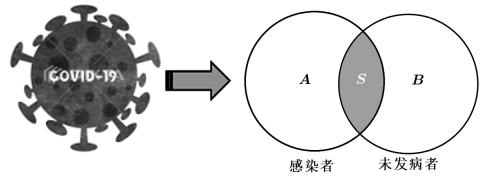

A、无症状感染者 B、发病者 C、未感染者 D、轻症感染者

查看试题解析
4. 要得到函数 $y = s i n （ 4 x -$ $\frac{π}{3}$ $）$ 的图象，只需要将函数 $y = s i n 4 x$ 的图象（）

A、向左平移 $\frac{π}{12}$ 个单位 B、向右平移 $\frac{π}{12}$ 个单位 C、向左平移 $\frac{π}{3}$ 个单位 D、向右平移 $\frac{π}{3}$ 个单位

查看试题解析
5. 已知函数 $f (x) = {\begin{array}{l} x + 2 ， x \leq 0 \\ x^{2} ， 0 < x \leq 3 \end{array}$ ，若 $f (x) = 9$ ，则x的值是（）

A、3 B、9 C、 $- 1$ 或1 D、 $- 3$ 或3

查看试题解析
6. 已知扇形的弧长是 $4 c m$ ，面积是 $2 c m^{2}$ ，则扇形的圆心角的弧度数是（）

A、1 B、2 C、4 D、1或4

查看试题解析
7. 已知函数 $f (x) = e^{x} - x^{2} + 8 x$ ，则在下列区间中 $f (x)$ 必有零点的是（）

A、(－2，－1) B、(－1，0) C、(0，1) D、(1，2)

查看试题解析
8. 下图是函数 $y = s i n (ω x + φ)$ 的部分图象，则 $s i n (ω x + ϕ) =$ （）

A、 $s i n (x + \frac{π}{3})$ B、 $s i n (\frac{π}{3} - 2 x)$ C、 $s i n (2 x + \frac{π}{6})$ D、 $s i n (2 x - \frac{π}{3})$

查看试题解析
9. 设 $a = 3^{0.7} ， b = {(\frac{1}{3})}^{- 0.8} ， c = \log_{0.7} 0.8$ ，则 $a ， b ， c$ 的大小关系为（）

A、 $a < b < c$ B、 $b < a < c$ C、 $b < c < a$ D、 $c < a < b$

查看试题解析
10. 设f(x)为偶函数，且在区间(－∞，0)上是增函数， $f (- 2) = 0$ ，则xf(x)＜0的解集为（）

A、(－1，0)∪(2，＋∞) B、(－∞，－2)∪(0，2) C、(－2，0)∪(2，＋∞) D、(－2，0)∪(0，2)

查看试题解析
11. 中国宋代的数学家秦九韶曾提出“三斜求积术”，即假设在平面内有一个三角形，边长分别为 $a, b, c$ ，三角形的面积S可由公式 $S = \sqrt{p (p - a) (p - b) (p - c)}$ 求得，其中 $p$ 为三角形周长的一半，这个公式也被称为海伦----秦九韶公式，现有一个三角形的边长满足 $a + b = 10, c = 8$ ，则此三角形面积的最大值为（）

A、6 B、9 C、12 D、18

查看试题解析
12. 设函数 $f (x) = \ln (1 + | x |) - \frac{1}{1 + x^{2}}$ ，则使 $f (x) > f (2 x - 1)$ 成立的 $x$ 的取值范围是（）

A、 $(\frac{1}{3} ， 1)$ B、 $(- \infty ， \frac{1}{3}) \cup (1 ， + \infty)$ C、 $(- \frac{1}{3} ， \frac{1}{3})$ D、 $(- \infty ， \frac{1}{3}) \cup (\frac{1}{3} ， + \infty)$

查看试题解析
13. 已知函数 $f (x) = {\begin{array}{l} (3 a - 1) x + 4 a ， x < 1 \\ l o g_{a} x ， x \geq 1 \end{array}$ 在 $R$ 上是减函数，则实数 $a$ 的取值范围是（）

A、 $(0 ， 1)$ B、 $(0 ， \frac{1}{3})$ C、 $[\frac{1}{7} ， \frac{1}{3})$ D、 $[\frac{1}{7} ， 1]$

查看试题解析

二、填空题

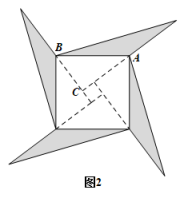
14. 2log₅10+log₅0.25= ．

查看试题解析
15. 如果二次函数 $f (x) = x^{2} - (a - 1) x + 5$ 在区间 $(\begin{array}{l} \frac{1}{2} ， 1 \end{array})$ 上是增函数，则实数 $a$ 的取值范围为．

查看试题解析
16. 已知 $\frac{\sin α - 2 \cos α}{3 \sin α + 5 \cos α}$ ＝－5，那么tanα＝.

查看试题解析
17. 如图1是我国古代著名的“赵爽弦图”的示意图，它由四个全等的直角三角形围成，其中 $s i n ∠ B A C = \frac{3}{5}$ ，现将每个直角三角形的较长的直角边分别向外延长一倍，得到如图2的数学风车，则图2“赵爽弦图”外面（图中阴影部分）的面积与大正方形面积之比为．

查看试题解析

三、解答题

18. 已知集合 $A = {x | a \leq x \leq a + 3}$ ， $B = {x | x < - 1$ 或 $x > 5}$ ．

(1)、若 $A ∩ B = \emptyset$ ，求a的取值范围；

(2)、若 $A ∩ B = A$ ，求a的取值范围．

查看试题解析
19. 已知角α的终边经过点P $(\frac{4}{5} ， - \frac{3}{5})$ .

(1)、求sinα的值；

(2)、求 $\frac{s i n (\frac{π}{2} - α) t a n (α - π)}{s i n (α + π) c o s (3 π - α)}$ 的值.

查看试题解析
20. 已知 $f (x)$ 是定义在 $[- 1 ， 1]$ 上的偶函数，且 $x \in [- 1 ， 0]$ 时， $f (x) = \frac{x}{x^{2} + 1}$ ．

(1)、求函数 $f (x)$ 的表达式；

(2)、判断并证明函数在区间 $[0 ， 1]$ 上的单调性．

查看试题解析
21. 某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品x万件，其总成本为 $G (x)$ 万元，其中固定成本为3万元，并且每生产1万件的生产成本为1万元（总成本=固定成本+生产成本），销售收入 $R (x)$ 满足 $R (x) = {\begin{array}{l} - x^{2} + 9 x ， 0 \leq x \leq 5 \\ 10 + x + \frac{25}{x} ， x > 5 \end{array}$ ，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，请完成下列问题：

(1)、写出利润函数 $y = f (x)$ 的解析式（利润=销售收入−总成本）；

(2)、工厂生产多少万件产品时，可使盈利最多？

查看试题解析
22. 已知函数 $f (x) = 2 \cos (ω x + φ) (ω > 0, | φ | < \frac{π}{2})$ 满足下列3个条件：
①函数 $f (x)$ 的周期为 $π$ ；② $x = \frac{π}{3}$ 是函数 $f (x)$ 的对称轴；③ $f (\frac{7 π}{12}) = 0$ .

(1)、请任选其中二个条件，并求出此时函数 $f (x)$ 的解析式；

(2)、若 $x \in [- \frac{π}{3}, \frac{π}{3}]$ ，求函数 $f (x)$ 的最值.

查看试题解析
23. 已知函数 $f (x) = l o g_{2} (2^{x} + 1) - k x$ 的图象过点 $(2 ， l o g_{2} \frac{5}{2})$ .

(1)、求实数 $k$ 的值；

(2)、若不等式 $f (x) + \frac{1}{2} x - a > 0$ 恒成立，求实数 $a$ 的取值范围；

(3)、若函数 $h (x) = 2^{f (x) + \frac{1}{2} x} + m \cdot 4^{x} - 1$ ， $x \in [0 ， l o g_{2} 3]$ ，是否存在实数 $m < 0$ 使得 $h (x)$ 的最小值为 $\frac{1}{2}$ ，若存在请求出 $m$ 的值；若不存在，请说明理由.

查看试题解析
24. 已知函数 $f (x) = a x^{2} - x + 2 a - 1$ （a为实常数）．

(1)、若 $a > 0$ ，设 $f (x)$ 在区间 $[1，2]$ 的最小值为 $g (a)$ ，求 $g (a)$ 的表达式：

(2)、设 $h (x) = \frac{f (x)}{x}$ ，若函数 $h (x)$ 在区间 $[1，2]$ 上是增函数，求实数a的取值范围．

查看试题解析