天津市南开区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-10-21 类型：期中考试

进入出卷网下载

一、单选题

1. 现实世界中，对称现象无处不在，中国的方块字中有些也只有对称性，下列汉字是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
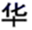2. 下列计算正确的是（）

A、b³•b³＝2b³ B、（a⁵）²＝a⁷ C、（﹣2a）²＝4a² D、（ab）⁵÷（ab）²＝ab³

查看试题解析
3. 下列各组条件中，能判定ΔABC≌ΔDEF的是（）

A、AB=DE ， BC=EF ， ∠A=∠D B、∠A=∠D ， ∠C=∠F ， AC=EF C、∠A=∠D ， ∠B=∠E ， ∠C=∠F D、AB=DE ， BC=EF ， ΔABC的周长＝ΔDEF的周长

查看试题解析
4. 如图，在Rt△ABC中，∠B＝90°，AD平分∠BAC，DE⊥AC于点E，则下列结错误的是（　　）

A、DE＝DB B、AE＝AB C、∠ADE＝∠ADB D、ED+BD＝BC

查看试题解析
5. 如图， $C D ⊥ A B$ ， $B E ⊥ A C$ ，垂足分别为点 $D$ ，点 $E$ ， $B E$ 、 $C D$ 相交于点O ， $∠ 1 = ∠ 2$ ，则图中全等三角形共有（）

A、2对 B、3对 C、4对 D、5对

查看试题解析
6. 计算：0.25²⁰²⁰×（﹣4）²⁰²¹＝（）。

A、﹣4 B、﹣1 C、1 D、4

查看试题解析
7. 如图，用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，那么第二步的作图痕迹②的作法是（）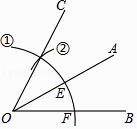

A、以点F为圆心，OE长为半径画弧 B、以点F为圆心，EF长为半径画弧 C、以点E为圆心，OE长为半径画弧 D、以点E为圆心，EF长为半径画弧

查看试题解析
8. 如图，在△ABC中，DM、EN分别垂直平分AB和AC，垂足为M，N．且分别交BC于点D，E．若∠DAE＝20°，则∠BAC的度数为（　　）

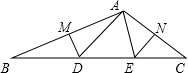A、100° B、105° C、110° D、120°

查看试题解析
9. 如图，为了测量B点到河对面的目标之间的距离，在B点同侧选择了一点C，测得 $∠ A B C = 75 °$ ， $∠ A C B = 35 °$ ，然后在M处立了标杆，使 $∠ C B M = 75 °$ ， $∠ M C B = 35 °$ ，得到 $△ M B C ≌ △ A B C$ ，所以测得 $M B$ 的长就是A，B两点间的距离，这里判定 $△ M B C ≌ △ A B C$ 的理由是（　　）

A、 $S A S$ B、 $A A S$ C、 $S S S$ D、 $A S A$

查看试题解析
10. 如图，正方形网格中，网格线的交点称为格点，已知A，B是两格点，如果C也是图中的格点，且使得 $△ ABC$ 为等腰三角形，则点C的个数有 $($ $)$

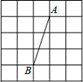A、4个 B、6个 C、8个 D、10个

查看试题解析
11. 图（1）是一个长为2m，宽为2n（m＞n）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（）

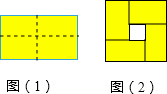A、2mn B、（m+n）² C、（m-n）² D、m²-n²

查看试题解析
12. 在数学活动课上，小明提出这样一个问题：∠B=∠C=90°，E是BC的中点，DE平分∠ADC，如图，则下列说法正确的有（　　）个．
⑴AE平分∠DAB；（2）△EBA≌△DCE；（3）AB+CD=AD；（4）AE⊥DE；（5）AB∥CD．

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 点P（﹣3，a）关于x轴的对称点是Q（b，﹣2），则ab的值为．

查看试题解析
14.
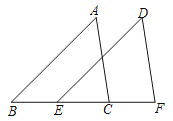
如图，点B、E、C、F在一条直线上，AB∥DE，且AB=DE，请添加一个条件，使△ABC≌△DEF．

查看试题解析
15. 如图，△ABC中，AB边上的垂直平分线DE交AB于D，交AC于E，AC＝9cm，△BCE的周长为15cm，则BC的长为cm．

查看试题解析
16. 已知a﹣b＝8，ab＝﹣15，则a²+b²＝．

查看试题解析
17. 如图所示，AD是△ABC的平分钱，DF⊥AB于点F，DE＝DG，若S△DEF＝2，S△ADG＝9：则△ADE的面积为．

查看试题解析
18. 如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，P、Q是边AC、BC上的两个动点， PD⊥AB于点D， QE⊥AB于点E．设点P、Q运动的时间是t秒（t＞0）．若点P从C点出发沿CA以每秒3个单位的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回到点C停止运动；点Q从点B出发沿BC以每秒1个单位的速度向点C匀速运动，到达点C后停止运动，当t=时，△APD和△QBE全等．

查看试题解析

三、解答题

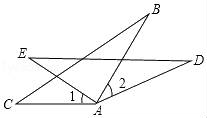
19. 计算：

(1)、（﹣3ab）²（ $\frac{1}{3}$ a⁴b³c²）÷（﹣3a³b²c²）

(2)、（a+2b）（a+b）﹣3a（a+b）

(3)、化简求值（2x+3y）²﹣（2x+y）（2x﹣y），其中 $x = \frac{1}{3}$ ， $y = \frac{1}{2}$ ．

查看试题解析
20. 如图所示，AC=AE，∠1=∠2，AB=AD．求证：BC=DE．

查看试题解析
21. 如图，在平面直角坐标系中，△ABC的三个顶点分别为A（2，3）、B（3，1）、C（﹣2，﹣2）．

(1)、请在图中作出△ABC关于y轴的轴对称图形△A′B′C′（A，B，C的对称点分别是A′，B′，C′），并直接写出A′，B′，C′的坐标．

(2)、求△A′B′C′的面积．

查看试题解析
22. 如图在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF⊥AC于点F．求证：∠B＝∠C．

查看试题解析
23. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D是AC上一点，过点A作BD的垂线交BD的延长线于点E，且BD＝2AE．
求证：

(1)、∠EAC＝∠DBC；

(2)、BD平分∠ABC．

查看试题解析
24. 如图，△ABC为等腰直角三角形，∠ACB＝90°，CA＝CB，点D在线段BC上，以AD为边作等腰直角三角形DAE，AD＝AE，∠DAE＝90°，过点E作EF⊥AC．

(1)、求证：△AEF≌△DAC；

(2)、如图2，连接BE，BE交AC点G，若BD＝2CD，求 $\frac{B D}{C G}$ 的值；

(3)、如图3，过点D作DP⊥AD交AB于点P，过点E作AE的垂线交AC的延长线于点H．连接PH，当点D在线段BC上运动时（不与点B，C重合），式子 $\frac{H E - D P}{H P}$ 的值是否发生变化？若不变，求出该值；若变化，请说明理由．

查看试题解析