山西省阳泉市盂县2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-10-21 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 以下是回收、绿色包装、节水、低碳四个标志，其中是轴对称图形的是（       ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是（   ）
    A、1,2,1 B、1,2,2 C、1,2,3 D、1,2,4

    查看试题解析

  • 3. 下列图形中，对称轴条数最少的是（　　）
    A、正五边形 B、正方形 C、等边三角形 D、圆

    查看试题解析

  • 4. 某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（   ）.

    A、带①去 B、带②去 C、带③去 D、①②③都带

    查看试题解析

  • 5. 如图，若 ∠1=110° ， ∠2=125° ，那么 ∠3 的度数为（    ）

    A、45° B、55° C、65° D、75°

    查看试题解析

  • 6. 一个正多边形的一个外角是72°，则这个多边形是（ ）
    A、三角形 B、五边形 C、六边形 D、七边形

    查看试题解析

  • 7. 如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（   ）


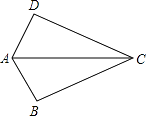    A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°

    查看试题解析

  • 8. 如图，在△ABC中，AC=AD=BD，∠B=35°，则∠CAD的度数为（   ）

    A、70° B、55° C、40° D、35°

    查看试题解析

  • 9. 如图，△ABC 中，AB=AC，AD 是∠BAC 的平分线，已知 AB=5，AD=3，则 BC的长为（   ）

    A、5 B、4 C、10 D、8

    查看试题解析

  • 10. 如图，在△ABC中AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是（   ）

    A、1 B、2 C、3 D、4

    查看试题解析

二、填空题

  • 11.

    如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是  ．

    查看试题解析

  • 12. 如图，将一副三角板如图摆放，则图中 ∠1 的度数是度．

    查看试题解析

  • 13. 如图△ABC中，∠B＝∠C，FD⊥BC，DE⊥AB，∠AFD＝158°，则∠EDF＝.

    查看试题解析

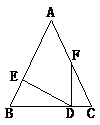  • 14. 如图是4×4正方形网络，其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形，这样的白色小方格有个.

    查看试题解析

  • 15. 如图，将长方形 ABCD 沿 DE 折叠，使点 A 落在 BC 边上的点 F 处，若 ∠EFB=50° ，则 ∠EDF 的度数为 ．

    查看试题解析

三、解答题

  • 16. 已知：如图，点A，B，C，D在同一直线上，AE∥DF，BF∥EC，AB=CD．求证：AE=DF.

     

    查看试题解析

  • 17. 如图，在△ABC中，AB＝AC ， AB的垂直平分线MN交AC于点D ， 交AB于点E ．

    (1)、若∠A＝40°，求∠DBC的度数；
    (2)、若AE＝6，△CBD的周长为20，求△ABC的周长．

    查看试题解析

  • 18. 如图，在平面直角坐标系中，A（3，4），B（1，2），C（5，1）．

    (1)、如图中作出△ABC关于y轴的对称图形△A1B1C1；
    (2)、写出点A1 ， B1 ， C1的坐标（直接写答案）．A1： ， B1： ， C1：；
    (3)、求△ABC的面积．

    查看试题解析

  • 19. 如图，Rt△ABC中，∠ACB＝90°，∠B＝50°，AD为∠BAC的平分线，F为AC上的点，DE⊥AB，垂足为E，DF＝DB．

    (1)、求证：DC＝DE；
    (2)、求证：△CDF≌△EDB；

    查看试题解析

  • 20. 已知，如图，△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90°，D为AB边上一点．

    (1)、求证：BD=AE．
    (2)、判断AD与AE的位置关系，并说明理由．

    查看试题解析

  • 21. 阅读下列材料，并完成任务．

    筝形的定义：两组邻边分别相等的四边形叫做筝形，几何图形的定义通常可作为图形的性质也可以作为图形的判定方法.也就是说，如图，若四边形ABCD是一个筝形，则AB=AD，BC=CD；若AB=AD，BC=CD，则四边形ABCD是筝形.

    如图，四边形ABCD是一个筝形，其中AB=AD，BC=CD．对角线AC，BD相交于点O，过点O作OM⊥AB，ON⊥AD，垂足分别为M，N.求证：四边形AMON是筝形.

    查看试题解析

  • 22. 我们在第十二章《全等三角形》中学习了全等三角形的性质和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题．例如：我们在解决：“如图1，在△ABC中，∠ACB=90° ， AC=BC ， 线段DE经过点C，且AD⊥DE于点D，BE⊥DE于点E．求证：AD=CE ， CD=BE”这个问题时，只要证明△ADC≌△CEB ， 即可得到解决，

    (1)、积累经验：

    请写出证明过程；

    (2)、类比应用：

    如图2，在平面直角坐标系中，△ABC中，∠ACB=90° ， AC=BC ， 点A的坐标为(0 ， 2) ， 点C的坐标为(1 ， 0) ， 求点B与x轴的距离．

    (3)、拓展提升：

    如图3，△ABC在平面直角坐标系中，∠ACB=90° ， AC=BC ， 点A的坐标为(2 ， 1) ， 点C的坐标为(4 ， 2) ， 求点B的坐标．

    查看试题解析

  • 23. 综合与探究

    [问题]如图1，在RtΔABC中，∠ACB=90∘ ， AC=BC ， 过点C作直线l平行于AB ， ∠EDF=90∘ ， 点D在直线l上移动，角的一边DE始终经过点B，另一边DF与AC交于点P，研究DP和DB的数量关系．

     

    (1)、[探究发现]

    如图2，某数学学习小组运用“从特殊到一般”的数学思想，发现当点D移动到使点P与点C重合时，很容易就可以得到DP=DB ， 请写出证明过程；

    (2)、[数学思考]

    如图3，若点P是AC上的任意一点(不含端点A、C)，受(1)的启发，另一个学习小组过点D，DG⊥CD交BC于点C，就可以证明DP=DB ， 请完成证明过程；

    (3)、[拓展引申]

    若点P是CA延长线上的任意一点，在图(4)中补充完整图形，并判断结论是否仍然成立．

    查看试题解析