山西省晋中市介休市2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-10-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，属于无理数的是（）

A、 $\frac{10}{3}$ B、π C、0 D、0.7654321

查看试题解析
2. 如图所示，笑脸盖住的点的坐标可能为（）

A、（5，2） B、（﹣2，3） C、（﹣4，﹣6） D、（3，﹣4）

查看试题解析
3. 我国是最早了解勾股定理的国家之一，早在三千多年前，周朝数学家商高就提出了“勾三、股四、弦五”这一结论，被记载于我国古代一部著名的数学著作中．这部著作是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{2}$ ÷ $\sqrt{3}$ ＝ $\frac{2 \sqrt{3}}{3}$ B、 $\sqrt{5}$ ﹣ $\sqrt{3}$ ＝ $\sqrt{2}$ C、 $\sqrt{2}$ × $\sqrt{3}$ ＝ $\sqrt{6}$ D、 $\sqrt{(- 3)^{2}}$ ＝﹣3

查看试题解析
5. 课间操时，小华、小军、小刚的位置如图，小华对小刚说，如果我的位置用（1，1）表示，小军的位置用（3，2）表示，那么你的位置可以表示成（）

A、（5，4） B、（4，5） C、（3，4） D、（4，3）

查看试题解析
6. 计算 $\sqrt{32} \times \sqrt{\frac{1}{2}} + \sqrt{2} \times \sqrt{5}$ 的结果估计在（）

A、 $8$ 与 $9$ 之间 B、 $10$ 与 $11$ 之间 C、 $7$ 与 $8$ 之间 D、 $9$ 与 $10$ 之间

查看试题解析
7. 如图，在数轴上点B表示的数为1，在点B的右侧作一个边长为1的正方形BACD，将对角线BC绕点B逆时针转动，使对角线的另一端落在数轴负半轴的点M处，则点M表示的数是（）

A、 $\sqrt{2}$ B、 $\sqrt{2}$ +1 C、1﹣ $\sqrt{2}$ D、﹣ $\sqrt{2}$

查看试题解析
8. 关于函数y＝﹣2x+1，下列结论正确的是（）

A、函数必经过点（﹣2，1） B、y随x的值增大而增大 C、与x轴交于（ $\frac{1}{2}$ ， 0） D、图象经过第一、二、三象限

查看试题解析
9. 如图所示，将一根长为24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，设筷子露在外面的长为hcm，则h的取值范围是（）

A、0＜h≤11 B、11≤h≤12 C、h≥12 D、0＜h≤12

查看试题解析
10. 李大爷要围成一个矩形菜园，菜园的一边利用足够长的墙，用篱笆围成的另外三边总长应恰好为24米．要围成的菜园是如图所示的矩形ABCD．设BC边的长为x米，AB边的长为y米，则y与x之间的函数关系式是（）

A、y=－2x+24(0<x<12) B、y=－ $\frac{1}{2}$ x＋12(0<x<24) C、y=2x－24(0<x<12) D、y= $\frac{1}{2}$ x－12(0<x<24)

查看试题解析

二、填空题

11. 计算 $\sqrt{45}$ ÷ $\sqrt{5}$ 的结果是．

查看试题解析
12. 如图是一片枫叶标本，其形状呈“掌状五裂型”，裂片具有少数突出的齿．将其放在平面直角坐标系中，表示叶片“顶部” $A$ ， $B$ 两点的坐标分别为 $(- 2 ， 2)$ ， $(- 3 ， 0)$ ，则叶杆“底部”点 $C$ 的坐标为．

查看试题解析
13. 如图所示，已知y与x满足正比例函数，则y与x的函数表达式为．

查看试题解析
14. 如图所示，有一块直角三角形纸片，∠C＝90°，AC＝8cm，BC＝6cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为cm．

查看试题解析
15. 如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要cm．

查看试题解析

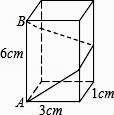
三、解答题

16. 计算：

(1)、 $\sqrt[3]{8} + (- \sqrt{2})^{2} - \sqrt{27} + | - \sqrt{3} |$ ；

(2)、 $\frac{\sqrt{8} \times \sqrt{18}}{\sqrt{2}} - \sqrt{6} \times \sqrt{\frac{9}{24}}$ ．

查看试题解析
17. 下面是小明同学进行实数运算的过程，认真阅读并完成相应的任务：
$\sqrt{\frac{7}{4}} + \sqrt{28} \div (\sqrt{7} - \frac{1}{\sqrt{7}})$
＝ $\frac{\sqrt{7}}{\sqrt{4}} + \sqrt{28} \div (\sqrt{7} - \frac{1}{\sqrt{7}})$ …第一步
＝ $\frac{\sqrt{7}}{2} + \sqrt{28} \div \sqrt{7} - \sqrt{28} \div \frac{1}{\sqrt{7}}$ …第二步
＝ $\frac{\sqrt{7}}{2} + 2 - \sqrt{28} \times \sqrt{7}$ …第三步
＝ $\frac{\sqrt{7}}{2} + 2 - 14$ …第四步
＝ $\frac{\sqrt{7}}{2} - 12$ …第五步

(1)、二次根式 $\sqrt{\frac{7}{4}}$ ， $\sqrt{28}$ ， $\sqrt{7}$ ， $\frac{1}{\sqrt{7}}$ 中，属于最简二次根式的是；

(2)、以上第一步的化简中由“ $\sqrt{\frac{7}{4}}$ ”化为“ $\frac{\sqrt{7}}{\sqrt{4}}$ ”所依据的数学公式是；

(3)、第步开始出现错误，写出该式的正确运算过程和结果．

查看试题解析
18. 如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．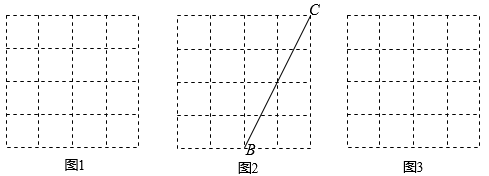

(1)、在图1中，画一个三角形，使它的三边长都是有理数；

(2)、在图2中，画一个以BC为斜边的直角三角形，使它们的三边长都是无理数且都不相等；

(3)、在图3中，画一个正方形，使它的面积是10．

查看试题解析
19. 如图是一副秋千架，左图是从正面看，当秋千绳子自然下垂时，踏板离地面0.5m（踏板厚度忽略不计），右图是从侧面看，当秋千踏板荡起至点B位置时，点B离地面垂直高度BC为1m，离秋千支柱AD的水平距离BE为1.5m（不考虑支柱的直径）.求秋千支柱AD的高.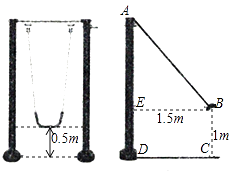

查看试题解析
20. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形） $A B C$ 的顶点A，B的坐标分别为 $(2 ， 4)$ ， $(- 1 ， 2)$ ．
（ 1 ）请在图中画出平面直角坐标系；
（ 2 ）请画出 $Δ A B C$ 关于x轴对称的 $Δ A^{'} B^{'} C^{'}$ ；
（ 3 ）线段 $B C^{'}$ 的长为．

查看试题解析
21. 观察下列等式：
① $\frac{1}{\sqrt{3} + 1} = \frac{\sqrt{3} - 1}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{\sqrt{3} - 1}{2}$ ；
② $\frac{1}{\sqrt{5} + \sqrt{3}} = \frac{\sqrt{5} - \sqrt{3}}{(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})} = \frac{\sqrt{5} - \sqrt{3}}{2}$ ；
③ $\frac{1}{\sqrt{7} + \sqrt{5}} = \frac{\sqrt{7} - \sqrt{5}}{(\sqrt{7} + \sqrt{5}) (\sqrt{7} - \sqrt{5})} = \frac{\sqrt{7} - \sqrt{5}}{2}$ ．
回答下列问题：

(1)、利用你观察到的规律，化简： $\frac{1}{5 + \sqrt{23}}$ ＝；

(2)、根据以上规律，写出第n个式子；

(3)、计算 $\frac{2}{1 + \sqrt{3}} + \frac{2}{\sqrt{3} + \sqrt{5}} + ⋯ + \frac{2}{\sqrt{2019} + \sqrt{2021}}$ 的结果为．

查看试题解析
22. 如图，在平面直角坐标系中，直线l₁：y＝ $\frac{1}{2}$ x+b与直线l₂：y＝2x相交于点B（m，4）．

(1)、求m，b的值；

(2)、直线l₁与y轴交于点M，求△AOM的面积；

(3)、过动点P（n，0）且垂于x轴的直线与l₁ ， l₂的交点分别为C，D，当点C位于点D上方时，直接写出n的取值范围．

查看试题解析
23. 在“综合与探究”课上，张老师让每名同学在练习本上画出一个长方形，随后以该长方形为基本图形，以小组为单位编制一道综合探究题．经过思考和讨论，励志小组向全班同学分享了他们编拟的试题，得到了侯老师的认可，同学们也眼前一亮，纷纷动手，开始了探究．请你也跟他们一起来完成这道试题吧．如图1，分别以长方形OABC的边OC，OA所在直线为x轴、y轴，建立平面直角坐标系，已知AO＝10，AB＝6，点E在线段OC上，以直线AE为轴，把△OAE翻折，点O的对应点D恰好落在线段BC上．

(1)、分别求点D，E的坐标．

(2)、如图2，若直线AD与x轴相交于点F，求直线AD表达式及点F的坐标．

(3)、在（2）的条件下，P是x轴上的一动点，是否存在以A，P，F为顶点的三角形是等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．

(4)、在本题的探究过程中，你感悟到哪些数学思想，请至少写出两条．

查看试题解析