内蒙古自治区赤峰市松山区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-10-21 类型：期中考试

进入出卷网下载

一、单选题

1. 斐波那契螺旋线也称为“黄金螺旋线”，它是根据斐波那契数列画出米的螺旋曲线，科学家在自然界中发现存在许多斐波那契螺旋线图案．下列斐波那契螺旋线图案中属于轴对称图形的是（）．

A、 B、 C、 D、

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ A = 80 °$ ，沿图中虚线截去 $∠ A$ ，则 $∠ 1 + ∠ 2 =$ （）

A、360° B、180° C、260° D、160°

查看试题解析
3. 如图， $△ A B C ≌ △ E D C$ ， $A C = 3 c m$ ， $D C = 5 c m$ ，则 $B E =$ （）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
4. 下列说法中，①三角形的内角中最多有一个钝角；②三角形的中线将三角形分成面积相等的两部分；③从n边形的一个顶点可以引 $(n - 3)$ 条对角线，把n边形分成 $(n - 2)$ 个三角形，因此，n边形的内角和是 $(n - 2) \cdot 180 °$ ；④全等三角形的面积一定相等．正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 平面直角坐标系有一点 $M (2 ， - 3)$ ，则点M关于y轴的对称点是（）

A、（2，3） B、（-2，3） C、（-2，-3） D、（-3，2）

查看试题解析
6. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（）

A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不符合题意

查看试题解析
7. 两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积= $\frac{1}{2}$ AC•BD，其中正确的结论有（）

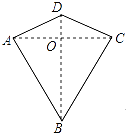A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 等腰三角形的一个内角是70°，则它的底角是（）

A、55° B、70° C、50°或70° D、70°或55°

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， BD是角平分线，若 $A C = 9 c m$ ， $A D ： C D = 2 ： 1$ ，则点D到AB的距离是（）

A、6cm B、5cm C、4cm D、3cm

查看试题解析
10. 如果等腰三角形的两边长分别为4cm和9cm，那么它的周长为（）

A、17cm B、13cm C、17cm或22cm D、22cm

查看试题解析
11. 如图，已知： $∠ M O N = 30 °$ ，点 $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ …在射线ON上，点 $B_{1}$ 、 $B_{2}$ 、 $B_{3}$ …在射线OM上， $△ A_{1} B_{1} A_{2}$ 、 $△ A_{2} B_{2} A_{3}$ 、 $△ A_{3} B_{3} A_{4}$ …均为等边三角形，若 $O A_{1} = 1$ ，则 $△ A_{6} B_{6} A_{7}$ 的边长为（）

A、16 B、32 C、64 D、128

查看试题解析
12. 如图，把长方形纸片ABCD沿对角线所在直线折叠，设重叠部分为 $△ E B D$ ，那么下列说法错误的是（）

A、 $△ E B D$ 是等腰三角形， $E B = E D$ B、折叠后 $∠ A B E$ 和 $∠ E B D$ 一定相等 C、折叠后得到的图形是轴对称图形 D、 $△ E B A$ 和 $△ E D C^{'}$ 一定是全等三角形

查看试题解析
13.
如图，四边形ABCD中，∠C=50°，∠B=∠D=90°，E、F分别是BC、DC上的点，当△AEF的周长最小时，∠EAF的度数为（　　）

A、50° B、60° C、70° D、80°

查看试题解析
14. 如图，D是 $△ A B C$ 的边BC上任意一点，E、F分别是线段AD、CE的中点，且 $△ A B C$ 的面积为 $20 c m^{2}$ ，则 $△ B E F$ 的面积是（） $c m^{2}$

A、15 B、10 C、5 D、2.5

查看试题解析

二、填空题

15. 分别剪一些边长相同的①正三角形、②正方形、③正五边形、④正六边形、⑤正八边形，如果用其中的一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图案（填序号即可）．

查看试题解析
16. 三个全等三角形按如图的形式摆放，则∠1+∠2+∠3的度数等于 .

查看试题解析
17. 如图，在△ABC中，AB＝AC＝4，∠A＝30°，那么S_△_ABC＝．

查看试题解析
18. 如图，在等边 $△ A B C$ 中，点D、E分别在边AB、BC上．把 $△ B D E$ 沿直线DE翻折，使点B落在点 $B^{'}$ 处， $D B^{'}$ 、 $E B^{'}$ 分别与AC交于点F、G．若 $∠ E D F = 50 °$ ，则 $∠ E G C =$ ．

查看试题解析

三、解答题

19. 已知边数为n的多边形的一个外角是m°，内角和是x°，外角和是y°．

(1)、当x＝2y时，求n的值；

(2)、若x+y+m＝2380，求m的值．

查看试题解析
20. 如图，小雅同学按以下步骤作∠AOB的平分线：
①以点O为圆心，任意长为半径作弧，交∠AOB的两边OA、OB于D、E两点；
②分别以点D、E为圆心，大于 $\frac{1}{2}$ DE的长为半径作弧，两弧交于点C；
③作射线OC，并连接CD、CE．
请根据以上材料完成下列问题：

(1)、完成下列证明过程（将符合题意答案填在相应的空上）
证明：由作图可知，在△OCD和△OCE中
${\begin{array}{l} O D = () \\ D C = () \\ O C = O C \end{array}$
∴△OCD≌△OCE（）
∴∠1＝∠2

(2)、求证：OC垂直平分DE．

查看试题解析
21. 如图，在 $Δ A B C$ 和 $Δ A D E$ 中， $A B = A D$ ， $A C = A E$ ， $∠ 1 = ∠ 2$ ， $A D$ 、 $B C$ 相交于点F．

(1)、求证： $∠ B = ∠ D$ ；

(2)、若 $A B$ // $D E$ ， $A E = 3$ ， $D E = 4$ ，求 $Δ A C F$ 的周长．

查看试题解析
22. 上午8时，一条船从海岛A出发，以每小时航行18海里的速度向正北航行，10时到达海岛B处，从A，B望灯塔C，测得灯塔C在A的北偏西15°，灯塔C在B的北偏西30°．

(1)、求从海岛B到灯塔C的距离；

(2)、在小灯塔C的周围20海里范围内有暗礁，如果轮船不改变方向继续向前航行，是否会有触礁危险？请说明理由．

查看试题解析
23. 已知：如图 $△ A B C$ 中， $∠ A = 90 °$ ， $A B = A C$ ， D是斜边BC的中点，E，F分别在线段AB，AC上，且 $∠ E D F = 90 °$ ．

(1)、求证： $△ D E F$ 为等腰直角三角形；

(2)、求证： $S_{四边形 A E D F} = S_{△ B D E} + S_{△ C D F}$ ；

(3)、如果点E运动到AB的延长线上，F在射线CA上且保持 $∠ E D F = 90 °$ ， $△ D E F$ 还仍然是等腰直角三角形吗？请画出图形直接写出结论．

查看试题解析
24. 【阅读理解】
课外兴趣小组活动时，老师提出了如下问题：
如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：

(1)、由已知和作图能得到△ADC≌△EDB的理由是____.

A、SSS B、SAS C、AAS D、HL

(2)、求得AD的取值范围是____.

A、6＜AD＜8 B、6≤AD≤8 C、1＜AD＜7 D、1≤AD≤7

(3)、【感悟】
解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF.求证：AC＝BF.

查看试题解析
25. 我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定．在一些探究题中经常用到以上知识转化角和边，进而解决问题．
问题初探：已知，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，点D为直线BC上一动点（点D不与点B、C重合），连接AD，以AD为直角边作等腰直角三角形ADE， $∠ D A E = 90 °$ ， $A D = A E$ ，连接CE．

(1)、如图1，当点D在线段BC上时，BD与CE的数量关系是， BD与CE的位置关系是， CE、BC、CD三条线段的数量关系是．

(2)、如图2，当点D在线段BC的延长线上时，其他条件不变，请写出CE、BC、CD三条线段之间的关系并说明理由．

(3)、如图3，当D运动到BC的延长线上时，若 $B C = 7$ ， $B D = 2$ ，求BE的长．

查看试题解析
26. 如图，在平面直角坐标系中，点O为坐标原点，点A、B、C的坐标分别为（0，6）、（-8，0）、（-3，0）， $A B = 10$ ，将 $△ A B C$ 沿着射线AC翻折，点B落到y轴上点D处．

(1)、求点D的坐标；

(2)、动点P以每秒1个单位长度的速度从点B出发沿着线段BO向终点O运动，运动时间为t秒，请用含有t的式子表示 $△ P C A$ 的面积，并直接写出t的取值范围；

(3)、在（2）的条件下，动点M以每秒2个单位长度的速度从点A出发沿着线段AO向终点O运动，动点N以每秒a个单位长度的速度从点O出发沿着x轴正方向运动，点P、M、N同时出发，点M停止时，点P、N也停止运动，当 $△ D O P ≌ △ M O N$ 时，求a的值．

查看试题解析