内蒙古乌海市海南区2020-2021学年八年级上学期期中考试数学试题
试卷更新日期：2022-10-21 类型：期中考试
一、单选题
-
1. 如图，下列图案是我国几家银行的标志，其中不是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知三条线段的长是：①2，2，4；②3，4，5；③3，3，7；④6，6，10.其中可构成三角形的有（ ）A、1个 B、2个 C、3个 D、4个3. 如图，AB∥CD，∠A＝38°，∠C＝80°，那么∠M等于（ ）
A、52° B、40° C、42° D、38°4. 如果等腰三角形的两边长为2cm，4cm，那么它的周长为（ ）A、8cm B、10cm C、11cm D、8cm或10cm5. 若一个多边形的每个外角都等于60°，则它的内角和等于（ ）
A、180° B、720° C、1080° D、540°6. 如图，△ABC中，AB=5，AC=8，BD，CD分别平分∠ABC，∠ACB，过点D作直线平行于BC，分别交AB，AC于E，F，则△AEF的周长为 （ ）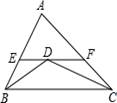
A、12 B、13 C、14 D、187. 如图所示，∠ACB＝∠DFE，BC＝EF，如果要使得△ABC≌△DEF，则还须补充的一个条件可以是（ ）
A、∠ABC＝∠DEF B、∠ACE＝∠DFB C、BF＝EC D、AB＝DE8. 如图，直线 ， ， 表示三条公路．现要建造一个中转站P，使P到三条公路的距离都相等，则中转站P可选择的点有（ ）
A、一处 B、二处 C、三处 D、四处9. 某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（ ）.
A、带①去 B、带②去 C、带③去 D、①②③都带10. 如图，∠B=∠D=90°，BC=CD，∠1=40°，则∠2=（ ）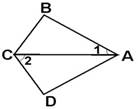
A、40° B、60° C、45° D、50°二、填空题
-
11. 如果等腰三角形的底角是 ， 那么这个三角形的顶角的度数是 ．12. △ABC中，AB＝AC，∠A＝∠C，则∠B＝度．13. 在平面直角坐标系中，点A（﹣4，8）关于x轴的对称点A′坐标 ．14. 一个多边形有9条对角线，则该多边形的内角和是 ．15. 如果△ABC≌△DEF，∠A＝40°，∠B＝55°，那么∠E＝.16. 如图，已知线段AB、CD相交于点O，且AO=BO，只需补充条件，则有△AOC≌△BOD．
17. 如图，根据SAS，如果AB＝AC， ， 即可判定ABD≌ACE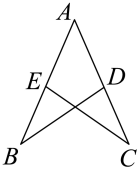
18. 如图，若∠A＝80°，∠ACD＝150°，则∠B＝度．
19. 如图，在△ABC中，∠C=90°，∠ABC的平分线BD交AC于点D．若BD=10厘米，BC=8厘米，DC=6厘米，则点D到直线AB的距离是厘米．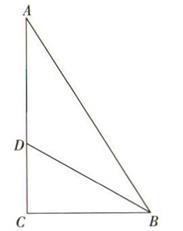
20. 如图，在中， ， ， 的垂直平分线交于D，交于E，则的周长等于 ．
三、解答题
-
21. 如图，AB＝AD ，∠BAD＝∠CAE，AC=AE ，求证：BC=DE
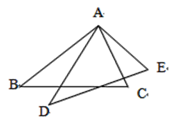22. 已知：如图，CE⊥AB，BF⊥AC，CE与BF相交于点D，且BD=CD.求证：点D在∠BAC的平分线上.
23. 如图，在△ABC中，AB＝AC，∠A＝36°，AB的垂直平分线MN交AC于点D，交AB于E．
(1)、求∠DBC的度数.(2)、猜想△BCD的形状并证明．24. 已知：如图，AD平分∠BAC ， DE⊥AB ， DF⊥AC ， DB=DC ，求证：BE=FC ．
25. ． 如图①，在△ABC 中，D、E 分别是 AB、AC 上的点，AB=AC，AD=AE，然后将△ADE 绕点 A 顺时针旋转一定角度，连接 BD，CE，得到图②，将 BD、CE 分别延长至 M、N，使 DM= BD，EN=CE，得到图③，请解答下列问题：
(1)、在图②中，BD 与 CE 的数量关系是；(2)、在图③中，猜想 AM 与 AN 的数量关系，∠MAN 与∠BAC 的数量关系，并证明你的猜想．26. 如图所示，在矩形ABCD中，AB＝6厘米，BC＝12厘米，点P沿AB边从点A开始向点B以1厘米/秒的速度移动，点Q沿BC从点B开始向点C以2厘米/秒的速度移动，如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6）．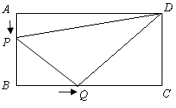
(1)、当PB＝2厘米时，求点P移动多少秒？(2)、t为何值时，△PBQ为等腰直角三角形？(3)、求四边形PBQD的面积，并探究一个与计算结果有关的结论．