江西省景德镇市2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-10-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数是无理数的是（）

A、 $\frac{π}{2}$ B、 ${(π - 1)}^{0}$ C、 $\frac{22}{7}$ D、3.14

查看试题解析
2. 下列四组线段中，构不成直角三角形的是（）

A、8，15，17 B、11，40，41 C、1.5，2，2.5 D、 $\sqrt{3}$ ， 2， $\sqrt{7}$

查看试题解析
3. 下列各实数比较大小，正确的是（）

A、 $\sqrt{6} < 2.3$ B、 $\sqrt{\frac{3}{2}} < 1$ C、 $- \sqrt{65} > - 8$ D、 $\frac{\sqrt{3} - 1}{3} < \frac{1}{3}$

查看试题解析
4. 景德镇市第十六中学为全面保障校庆五十周年的整体效果，在操场中标记了几个关键位置，如图是利用平面直角坐标系画出的关键位置分布图，若表示点A的坐标为 $(- 1 ， - 2)$ ，点B的坐标为 $(1 ， 1)$ ，则表示其他位置的点的坐标正确的是（）

A、 $C (- 1 ， - 2)$ B、 $D (- 3 ， 1)$ C、 $E (- 7 ， - 3)$ D、 $F (4 ， - 1)$

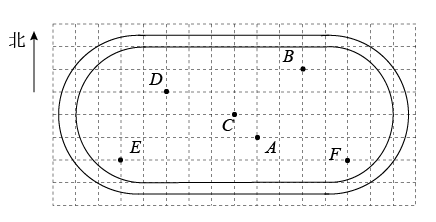查看试题解析
5. 在如图所示的赵爽弦图中，在DH上取点M使得DM＝GH，连接AM、CM．若正方形EFGH的面积为10，则△ADM与△CDM的面积之差为（）

A、5 B、4 C、 $\sqrt{5}$ D、不确定

查看试题解析
6. 如图在4×5的网格中，每个小正方形的边长都是1个单位长度，定义：以网格中小正方形顶点为顶点的正方形叫作格点正方形，图中包含“△”的格点正方形有（）个．

A、11 B、15 C、16 D、17

查看试题解析

二、填空题

7. $\sqrt{16}$ 的算术平方根是

查看试题解析
8. 当 $x = 1 + \sqrt{2}$ 时，代数式 $x^{2} - 2 x + 2021 =$ ．

查看试题解析
9. 已知a、b满 $\sqrt{a - 1} + (b + 3)^{2} = 0$ ，则点 $M (a ， b)$ 关于y轴对称的点的坐标为．

查看试题解析
10. 《九章算术》是我国古代数学名著，书中有下列问题：“今有户高多于广六尺八寸，两隅相去适一丈.问户高、广各几何？”其意思为：今有一门，高比宽多6尺8寸，门对角线距离恰好为1丈.问门高、宽各是多少？（1丈＝10尺，1尺＝10寸）如图，设门高 $A B$ 为 $x$ 尺，根据题意，可列方程为.

查看试题解析
11. 如图，在平面直角坐标系中，点B的坐标为 $(3 ， 1)$ ， $A B = O B$ ， $∠ A B O = 90 °$ ，则点A的坐标是．

查看试题解析
12. 如图，Rt△ACB中，∠ACB=90°，AB=13cm，AC=5cm，动点P从点B出发沿射线BC以2cm/s的速度运动，设运动时间为ts，当△APB为等腰三角形时，t的值为．

查看试题解析

三、解答题

13. 解下列方程：

(1)、 $3 x^{2} - 27 = 0$

(2)、 $\frac{{(x - 2)}^{3}}{8} = - 125$

查看试题解析
14. 计算：

(1)、 $4 \sqrt{\frac{1}{2}} - \sqrt{6} \times \sqrt{3} + \sqrt{12} \div \sqrt{3}$

(2)、 $\sqrt[3]{- 27} - \sqrt{{(- 2)}^{2}} + {(\frac{1}{2})}^{- 2} - | 1 - \sqrt{3} |$

查看试题解析
15. 已知点 $P (a + 1 ， 2 a - 3)$ ，分别根据下列条件求出点P的坐标．

(1)、点P在y轴上；

(2)、点P到两坐标轴的距离相等．

查看试题解析
16. 定义：在边长为1的小正方形方格纸中，把顶点落在方格交点上的线段、三角形、四边形分别称为格点线段、格点三角形、格点四边形，请按要求画图：

(1)、在图1中画出一条长为5，且不与正方形方格纸的边平行的格点线段AB；

(2)、在图2中画出一个面积为13的格点正方形CDEF．

查看试题解析
17. 2021年是中国共产党建党100周年，大街小巷挂满了彩旗．如图是一面长方形彩旗完全展平时的尺寸图（单位：cm）．其中长方形ABCD是由双层白布缝制的穿旗杆用的旗裤，阴影部分DCEF为长方形绸缎旗面，将穿好彩旗的旗杆垂直插在地面上．旗杆从旗顶到地面的高度为240cm，在无风的天气里，彩旗自然下垂．求彩旗下垂时最低处离地面的最小高度h．

查看试题解析
18. 已知2a＋2的立方根是－2，a＋b＋4的算术平方根是3，c是 $\sqrt{15}$ 的整数部分．

(1)、求a，b，c的值．

(2)、求 $a^{2} - a b + 2 c$ 的平方根．

查看试题解析
19. 如图，△ABC的三边分别为AC＝5，BC＝12，AB＝13，将△ABC沿AD折叠，使AC落在AB上，求折痕AD的长．

查看试题解析
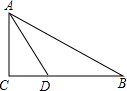20. 如图，已知圆柱底面的周长为12，圆柱的高为8，在圆柱的侧面上，过点A，C嵌有一圈长度最短的金属丝．

(1)、现将圆柱侧面沿AB剪开，所得的圆柱侧面展开图是．

(2)、如图①，求该长度最短的金属丝的长．

(3)、如图②，若将金属丝从点B绕四圈到达点A，则所需金属丝最短长度是多少？

查看试题解析
21. 观察下列一组式的变形过程，然后回答问题：
例1： $\frac{1}{\sqrt{2} + 1} = \frac{(\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{{(\sqrt{2})}^{2} - 1} = \frac{\sqrt{2} - 1}{1} = \sqrt{2} - 1$ ，
例2： $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}} = \sqrt{4} - \sqrt{3}$ ， $\frac{1}{\sqrt{5} + \sqrt{4}} = \sqrt{5} - \sqrt{4} \dots$ ，

(1)、 $\frac{1}{\sqrt{6} + \sqrt{5}} =$ ； $\frac{1}{\sqrt{2022} + \sqrt{2021}} =$ ．

(2)、请你用含n（n为正整数）的关系式表示上述各式子的变形规律．

(3)、利用上面的结论，求下列式子的值 $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{2022} + \sqrt{2021}}) \times (\sqrt{2022} + 1)$ ．

查看试题解析
22. 如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连接AC，EC．已知AB＝5，DE＝1，BD＝8，设CD＝x．

(1)、用含x的代数式表示AC＋CE的长；

(2)、请问点C满足什么条件时AC＋CE的值最小？求出最小值．

(3)、根据（2）中的结论，请构图求出代数式 $\sqrt{x^{2} + 9} + \sqrt{{(24 - x)}^{2} + 16}$ 的最小值．

查看试题解析
23. 如图， $A (- 1 ， 0)$ ， $C (1 ， 4)$ ，点B在x轴的正半轴上，且AB＝4，连接AC交y轴于点D．

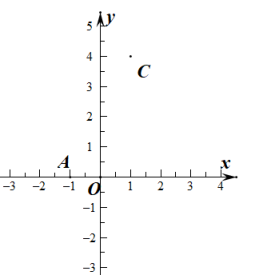(1)、求点B与点D的坐标；

(2)、在y轴上是否存在点P，使得△ACP的面积与△ABC的面积相等？若存在，请求出点P的坐标；若不存在，请说明理由；

(3)、若点Q的纵坐标为5，且△QBC面积为20，请求出点Q的坐标．

查看试题解析