河北省石家庄市赞皇县2021-2022学年八年级上学期期中考试数学试题
试卷更新日期:2022-10-21 类型:期中考试
一、单选题
-
1.
下列图形中,不是运用三角形的稳定性的是( )
 A、房屋顶支撑架 B、自行车三脚架 C、拉闸门 D、木门上钉一根木条2. △ABC中,AB=3,AC=2,BC=a,下列数轴中表示的a的取值范围,正确的是( )A、
A、房屋顶支撑架 B、自行车三脚架 C、拉闸门 D、木门上钉一根木条2. △ABC中,AB=3,AC=2,BC=a,下列数轴中表示的a的取值范围,正确的是( )A、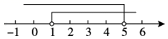 B、
B、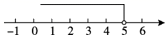 C、
C、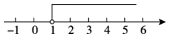 D、
D、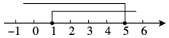 3. 下列图形是轴对称图形的是( )A、
3. 下列图形是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 一个三角形有两个内角的度数分别为和 , 则这个三角形属于( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定5. 平面直角坐标系中,点关于y轴的对称点坐标是( )A、 B、 C、 D、6. 如图,ΔABC≌ΔDCB,若AC=7,BE﹦5,则DE的长为( )
4. 一个三角形有两个内角的度数分别为和 , 则这个三角形属于( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定5. 平面直角坐标系中,点关于y轴的对称点坐标是( )A、 B、 C、 D、6. 如图,ΔABC≌ΔDCB,若AC=7,BE﹦5,则DE的长为( )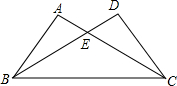 A、2 B、3 C、4 D、57. 如图,是的中线,已知的周长为 , 比长 , 则的周长为( )
A、2 B、3 C、4 D、57. 如图,是的中线,已知的周长为 , 比长 , 则的周长为( )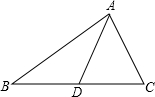 A、 B、 C、 D、8. 在下列说法中,正确的个数有( ).
A、 B、 C、 D、8. 在下列说法中,正确的个数有( ).①三角对应相等的两个三角形全等 ②两角、一边对应相等的两个三角形全等
③三边对应相等的两个三角形全等 ④两边、一角对应相等的两个三角形全等
A、1个 B、2个 C、3个 D、4个9. 小强从镜子中看到的电子表的读数如图所示,则电子表的实际读数是( ) A、15:01 B、10:51 C、10:21 D、10:1510. 如图,直线 , 若 , 则的度数为( )
A、15:01 B、10:51 C、10:21 D、10:1510. 如图,直线 , 若 , 则的度数为( )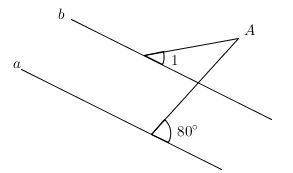 A、 B、 C、 D、11. 一个多边形每个外角都等于 , 则从这个多边形的某个顶点画对角线,最多可以画出几条( )A、7条 B、8条 C、9条 D、10条12. 如图,是的角平分线,C为上一点,于E, , 在射线上有一动点Q,则在运动过程中,点Q到点C的最短距离是( )
A、 B、 C、 D、11. 一个多边形每个外角都等于 , 则从这个多边形的某个顶点画对角线,最多可以画出几条( )A、7条 B、8条 C、9条 D、10条12. 如图,是的角平分线,C为上一点,于E, , 在射线上有一动点Q,则在运动过程中,点Q到点C的最短距离是( ) A、6 B、4 C、2 D、不能确定13. 如图,已知 , 那么的度数是( )
A、6 B、4 C、2 D、不能确定13. 如图,已知 , 那么的度数是( )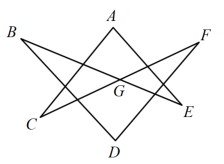 A、180° B、280° C、320° D、360°14. 如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
A、180° B、280° C、320° D、360°14. 如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( ) A、2个 B、3个 C、4个 D、5个15. 已知等腰中,于D,且 , 则底角的度数为( )A、45° B、75°或45° C、45°或30° D、75°或45°或15°16. 如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论:①BD=CD;②AD+CF=BD;③CE= BF;④AE=BG.其中正确的是( )
A、2个 B、3个 C、4个 D、5个15. 已知等腰中,于D,且 , 则底角的度数为( )A、45° B、75°或45° C、45°或30° D、75°或45°或15°16. 如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论:①BD=CD;②AD+CF=BD;③CE= BF;④AE=BG.其中正确的是( )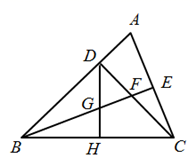 A、①② B、①③ C、①②③ D、①②③④
A、①② B、①③ C、①②③ D、①②③④二、填空题
-
17. 若等腰三角形的一个角为80°,则底角为.18. 在平面直角坐标系中,如果点和关于x轴对称,则: , .19. 下图是某工人加工的一个机器零件(数据如图),经过测量不符合标准.标准要求是: , 且、、保持不变为了达到标准,工人在保持不变情况下,应将图中(填“增大”或“减小”)度.

三、解答题
-
20. 一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和内角和.21. A,B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3),根据下列要求作图(保留作图痕迹,不用写作法).

( 1 )一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A,B两校的距离相等?如果有,请用尺规作图找出该点;
( 2 )若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置.
22. 如图,ABC的面积为30,AD是ABC的中线,BE是ABD的中线,EF⊥BC于点F.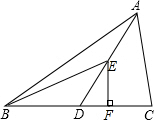 (1)、求BDE的面积.(2)、若EF=5,求CD的长.23. 如图,已知三个顶点的坐标分别为 .
(1)、求BDE的面积.(2)、若EF=5,求CD的长.23. 如图,已知三个顶点的坐标分别为 .
( 1 )将先向右平移4个单位,再向下平移3个单位后,得到 , 点A,B,C的对应点分别为、、 . 根据要求在网格中画出相应图形并写出对应点坐标( )、( )、( );
( 2 )画出关于y轴的对称图形 , 点、、的对应点分别为、、 , 则各对应点的坐标分别为( )、( )、( ).
24. 如图,中, , 垂足为D. , 垂足为G, , . (1)、求证:;(2)、求的度数.25. ABCD为一张长方形纸片,AB//CD,AD//BC,∠A=∠B=∠C=∠D=90°,观察折叠后的结果,并回答问题.
(1)、求证:;(2)、求的度数.25. ABCD为一张长方形纸片,AB//CD,AD//BC,∠A=∠B=∠C=∠D=90°,观察折叠后的结果,并回答问题.
 (1)、如图1,沿DE折叠长方形纸片,使点C落在AD上点C'处,CD恰好与AD在同一直线上,则∠C'ED=°,△C'ED为三角形.(2)、如图2,沿EF折叠长方形纸片,使EF=PE,折叠后点C,D分别落在点C',D'处,C'E与AD相交于点P.求证:△PEF为等边三角形.26. 如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
(1)、如图1,沿DE折叠长方形纸片,使点C落在AD上点C'处,CD恰好与AD在同一直线上,则∠C'ED=°,△C'ED为三角形.(2)、如图2,沿EF折叠长方形纸片,使EF=PE,折叠后点C,D分别落在点C',D'处,C'E与AD相交于点P.求证:△PEF为等边三角形.26. 如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线. (1)、求∠ACB的大小;(2)、如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;(3)、如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.
(1)、求∠ACB的大小;(2)、如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;(3)、如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.