河北省石家庄市新乐市2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-10-21 类型:期中考试
一、单选题
-
1. 下列式子中分式的是( )A、 B、 C、 D、2. 若分式 无意义,则( ).A、 B、 C、 D、3. 下列实数中,最大的数是( )A、 B、 C、 D、34. 下列各式中,没有平方根的是( )A、-22 B、(-2)2 C、-(-2) D、∣-2∣5. 把分式中的x,y都扩大为原来的10倍,则分式的值( )A、扩大为原来的10倍 B、分式的值不变 C、缩小为原来的 D、不能确定6. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
 A、40° B、30° C、35° D、25°7. 已知2a+1和5是正数b的两个平方根,则a+b的值是( )A、25 B、30 C、20 D、228. 计算 的结果是( )A、3 B、 C、1 D、9. 估计30的立方根在哪两个整数之间( )A、2与3 B、3与4 C、4与5 D、5与610. 下列说法错误的是( )A、有两条边和它们的夹角对应相等的两个三角形全等 B、有三个角对应相等的两个三角形全等 C、有两个角及其中一角的对边对应相等的两个三角形全等 D、有三条边对应相等的两个三角形全等11. 方程 的解是( )A、 B、 C、 D、12. 如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.那么C,D两点间的距离就是在A点处小明与游艇的距离.在这个问题中,可作为证明的依据的是( )
A、40° B、30° C、35° D、25°7. 已知2a+1和5是正数b的两个平方根,则a+b的值是( )A、25 B、30 C、20 D、228. 计算 的结果是( )A、3 B、 C、1 D、9. 估计30的立方根在哪两个整数之间( )A、2与3 B、3与4 C、4与5 D、5与610. 下列说法错误的是( )A、有两条边和它们的夹角对应相等的两个三角形全等 B、有三个角对应相等的两个三角形全等 C、有两个角及其中一角的对边对应相等的两个三角形全等 D、有三条边对应相等的两个三角形全等11. 方程 的解是( )A、 B、 C、 D、12. 如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.那么C,D两点间的距离就是在A点处小明与游艇的距离.在这个问题中,可作为证明的依据的是( ) A、或 B、或 C、或 D、或13. 某玩具厂要生产a只吉祥物“欢欢”,原计划每天生产b只,实际每天生产了(b+c)只,则该厂提前完成任务的天数是( )A、 B、 C、 D、14. 如图,在 和 中, ,添加一个条件,不能证明 和 全等的是( )
A、或 B、或 C、或 D、或13. 某玩具厂要生产a只吉祥物“欢欢”,原计划每天生产b只,实际每天生产了(b+c)只,则该厂提前完成任务的天数是( )A、 B、 C、 D、14. 如图,在 和 中, ,添加一个条件,不能证明 和 全等的是( ) A、 B、 C、 D、15. 如图,在 和 中, , , , .连接 、 交于点M,连接 .下列结论:
A、 B、 C、 D、15. 如图,在 和 中, , , , .连接 、 交于点M,连接 .下列结论: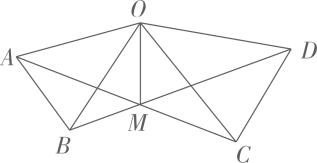
① ;② ;③ 平分 ;④ 平分
其中正确的结论个数有( )个.
A、4 B、3 C、2 D、116. 若(a不取0和-1), , , …, , 则等于( )A、 B、 C、 D、二、填空题
-
17. 21的平方根是 .18. 如图, , ,要使 ≌ ,只需增加一个条件,这个条件可以是 .
 19. 对于关于x的分式方程
19. 对于关于x的分式方程①若k=1,则方程的解为;
②若方程有增根且无解,则k的值为;
③若方程的解为负数,请你写出符合条件的且互为相反数的两个k的值 .
三、解答题
-
20. 把下列各数填在相应的大括号里: , , 0, , +5, , , 3.24,-3.1415.
整数:{ …};
负分数:{ …};
无理数:{ …}.
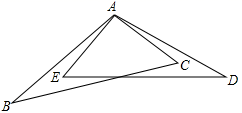
21. 如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°. (1)、求线段AE的长.(2)、求∠DBC的度数.22. 如图,已知 ,
(1)、求线段AE的长.(2)、求∠DBC的度数.22. 如图,已知 , (1)、求作: , 使得 .(2)、完成下面证明过程(将符合题意答案填在相应的空内):
(1)、求作: , 使得 .(2)、完成下面证明过程(将符合题意答案填在相应的空内):证明:由作图可知,在和中,
∴
(3)、这种作一个三角形与已知三角形全等的方法的依据是 .23. 计算(1)、;(2)、;(3)、 .24. 先化简,再求值: ,其中m是已知两边分别为2和3的三角形的第三边长,且m是整数.25. 六一儿童节来临之际,某商店用3000元购进一批玩具,很快售完;第二次购进时,每件的进价提高了20%,同样用3000元购进的数量比第一次少了10件.(1)、求第一次每件的进价为多少元?(2)、若两次购进的玩具售价均为70元,且全部售完,求两次的总利润为多少元?26. (1)、如图①,已知: 中, , ,直线m经过点A, 于D, 于E,求证: ;(2)、拓展:如图②,将(1)中的条件改为: 中, ,D、A、E三点都在直线m上,并且 , 为任意锐角或钝角,请问结论 是否成立?如成立,请证明;若不成立,请说明理由;(3)、应用:如图③,在 中, 是钝角, , , ,直线m与BC的延长线交于点F,若 , 的面积是12,求 与 的面积之和.
(1)、如图①,已知: 中, , ,直线m经过点A, 于D, 于E,求证: ;(2)、拓展:如图②,将(1)中的条件改为: 中, ,D、A、E三点都在直线m上,并且 , 为任意锐角或钝角,请问结论 是否成立?如成立,请证明;若不成立,请说明理由;(3)、应用:如图③,在 中, 是钝角, , , ,直线m与BC的延长线交于点F,若 , 的面积是12,求 与 的面积之和.