河北省保定市雄县2021-2022学年八年级上学期期中质量反馈训练数学试题
试卷更新日期:2022-10-21 类型:期中考试
一、单选题
-
1. 下列四个汉字中,可看成是轴对称图形的是( )A、爱 B、我 C、中 D、华2. 如图,若是的中线, , 则的长度为( )
 A、2 B、3 C、4 D、83. 点A(2,﹣1)关于y轴对称的点的坐标为( )A、(﹣2,﹣1) B、(2,1) C、(﹣2,1) D、(1,2)4. 如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是( )
A、2 B、3 C、4 D、83. 点A(2,﹣1)关于y轴对称的点的坐标为( )A、(﹣2,﹣1) B、(2,1) C、(﹣2,1) D、(1,2)4. 如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是( ) A、ASA B、SAS C、AAS D、SSS5. 已知的三边分别为a,b,c,若 , c的长为偶数,则满足条件的c的值有( )A、1个 B、2个 C、3个 D、5个6. 如图, , 点B,C,E在同一条直线上,且 , 则的长为( )
A、ASA B、SAS C、AAS D、SSS5. 已知的三边分别为a,b,c,若 , c的长为偶数,则满足条件的c的值有( )A、1个 B、2个 C、3个 D、5个6. 如图, , 点B,C,E在同一条直线上,且 , 则的长为( ) A、10 B、11 C、12 D、137. 如图,在的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰1个白色的小正方形,使新构成灰色部分的图形是轴对称图形,满足条件的小正方形有( )
A、10 B、11 C、12 D、137. 如图,在的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰1个白色的小正方形,使新构成灰色部分的图形是轴对称图形,满足条件的小正方形有( ) A、3个 B、2个 C、1个 D、0个8. 如图,是的外角的平分线,若 , , 则的度数为( )
A、3个 B、2个 C、1个 D、0个8. 如图,是的外角的平分线,若 , , 则的度数为( ) A、 B、 C、 D、9. 如图,直线l是线段的垂直平分线,点C在直线l外,且与点A在直线l的同一侧,P是直线l上的任意点,连接 , , , 则与的大小关系是( )
A、 B、 C、 D、9. 如图,直线l是线段的垂直平分线,点C在直线l外,且与点A在直线l的同一侧,P是直线l上的任意点,连接 , , , 则与的大小关系是( ) A、 B、 C、 D、10. 如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A、 B、 C、 D、10. 如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )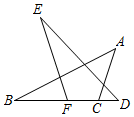 A、∠B=∠E B、AC=DF C、∠ACD=∠BFE D、BC=EF11. 如图,已知直线AB和AB上的一点C , 过点C作直线AB的垂线,步骤如下:
A、∠B=∠E B、AC=DF C、∠ACD=∠BFE D、BC=EF11. 如图,已知直线AB和AB上的一点C , 过点C作直线AB的垂线,步骤如下:第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以 为半径作弧,两弧交于点F;
第三步:作直线CF , 直线CF即为所求.
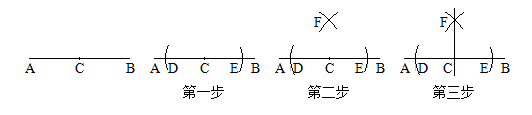
下列关于 的说法正确的是( )
A、 ≥ B、 ≤ C、 D、12. 如图,是等腰三角形,点O是底边上任意一点,、分别与两边垂直,等腰三角形的腰长为6,面积为15,则的值为( ) A、 B、 C、 D、13. 为测量一池塘两端A,B间的距离,甲、乙两位同学分别设计了两种不同的方案.
A、 B、 C、 D、13. 为测量一池塘两端A,B间的距离,甲、乙两位同学分别设计了两种不同的方案.甲:如图1,先过点B作的垂线 , 再在射线上取C,D两点,使 , 接着过点D作的垂线 , 交的延长线于点E,则测出的长即为A,B间的距离;
乙:如图2,先确定直线 , 过点B作射线 , 在射线上找可直接到达点A的点D,连接 , 作 , 交直线于点C,则测出的长即为A,B间的距离,则下列判断正确的是( )
 A、只有甲同学的方案可行 B、只有乙同学的方案可行 C、甲、乙同学的方案均可行 D、甲、乙同学的方案均不可行14. 如图,已知在中, , , , 的三条角平分线交于点O,则等于( )
A、只有甲同学的方案可行 B、只有乙同学的方案可行 C、甲、乙同学的方案均可行 D、甲、乙同学的方案均不可行14. 如图,已知在中, , , , 的三条角平分线交于点O,则等于( ) A、 B、 C、 D、15. 如图,在中, , P为内一点,过点P的直线分别交 , 于点E,F,若点E,F分别在 , 的垂直平分线上,则的度数为( )
A、 B、 C、 D、15. 如图,在中, , P为内一点,过点P的直线分别交 , 于点E,F,若点E,F分别在 , 的垂直平分线上,则的度数为( ) A、 B、 C、 D、16. 如图,在中, , , . 点P从点A出发,以每秒2个单位长度的速度沿折线向终点B运动,同时点Q从点B出发,以每秒3个单位长度的速度沿折线向终点A运动,点P,Q都运动到各自的终点时停止.设运动时间为t(秒).直线l经过点C,且 , 过点P、Q分别作直线l的垂线段,垂足为E,F,当与全等时,t的值可能是( )
A、 B、 C、 D、16. 如图,在中, , , . 点P从点A出发,以每秒2个单位长度的速度沿折线向终点B运动,同时点Q从点B出发,以每秒3个单位长度的速度沿折线向终点A运动,点P,Q都运动到各自的终点时停止.设运动时间为t(秒).直线l经过点C,且 , 过点P、Q分别作直线l的垂线段,垂足为E,F,当与全等时,t的值可能是( ) A、2 B、3 C、4 D、6
A、2 B、3 C、4 D、6二、填空题
-
17. 有公共边的正五边形和正六边形按如图所示的位置摆放,延长交正六边形于点F.
 (1)、的度数为;(2)、的度数为 .18. 如图,△ABC是等边三角形,BC=BD,∠BAD=20°,则∠BCD的度数为 .
(1)、的度数为;(2)、的度数为 .18. 如图,△ABC是等边三角形,BC=BD,∠BAD=20°,则∠BCD的度数为 . 19. 如图,在中, , D是边上一点,平分 .
19. 如图,在中, , D是边上一点,平分 .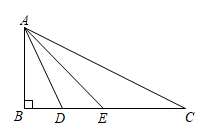 (1)、若 , , 的度数为;(2)、若 , , 的度数为 . (用含m,n的式子表示)
(1)、若 , , 的度数为;(2)、若 , , 的度数为 . (用含m,n的式子表示)三、解答题
-
20. 如图,已知在四边形中, , .
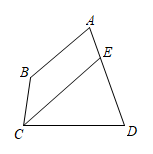 (1)、的度数为;(2)、若的平分线交边于点E,且 , 求的度数.21. 如图,已知 , 且点B,C,D在同一条直线上,延长交于点F.
(1)、的度数为;(2)、若的平分线交边于点E,且 , 求的度数.21. 如图,已知 , 且点B,C,D在同一条直线上,延长交于点F. (1)、求证:;(2)、已知 , , 求的长度.22. 如图,已知线段 , 在平面直角坐标系中,且点A的坐标为 .
(1)、求证:;(2)、已知 , , 求的长度.22. 如图,已知线段 , 在平面直角坐标系中,且点A的坐标为 . (1)、请在图中画出线段关于x轴对称的线段 , 并写出点的坐标;(2)、请在图中画出直线l,使得直线l是线段和线段的对称轴;(3)、在(2)的基础上,用无刻度的直尺和圆规在直线l上找一点P,使得 . (保留作图痕迹,不要求写作法)23. 如图,在中, , 点D在边上,过点D作 , , 且 .
(1)、请在图中画出线段关于x轴对称的线段 , 并写出点的坐标;(2)、请在图中画出直线l,使得直线l是线段和线段的对称轴;(3)、在(2)的基础上,用无刻度的直尺和圆规在直线l上找一点P,使得 . (保留作图痕迹,不要求写作法)23. 如图,在中, , 点D在边上,过点D作 , , 且 . (1)、若 , 求的度数;(2)、求证: .24. 在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F.
(1)、若 , 求的度数;(2)、求证: .24. 在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F. (1)、求证:△ABD是等边三角形;(2)、求证:BE=AF.
(1)、求证:△ABD是等边三角形;(2)、求证:BE=AF.

