江苏省南通市海安市2021-2022学年高一上学期数学期末考试试卷
试卷更新日期:2022-10-21 类型:期末考试
一、单选题
-
1. 已如集合 , , , 则( )A、 B、 C、 D、2. 已知为角终边上一点,则( )A、 B、1 C、2 D、33. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,4. 图1是南北方向、水平放置的圭表(一种度量日影长的天文仪器,由“圭”和“表”两个部件组成)示意图,其中表高为h,日影长为l.图2是地球轴截面的示意图,虚线表示点A处的水平面.已知某测绘兴趣小组在冬至日正午时刻(太阳直射点的纬度为南纬)在某地利用一表高为的圭表按图1方式放置后,测得日影长为 , 则该地的纬度约为北纬( )(参考数据: , )
 A、 B、 C、 D、5. 若 , 的终边(均不在y轴上)关于x轴对称,则( )A、 B、 C、 D、6. 设P为函数的图象上一点,O为坐标原点,则的最小值为( )A、2 B、 C、 D、7. , , , 则( )A、 B、 C、 D、8. 函数的图象可能是( )A、
A、 B、 C、 D、5. 若 , 的终边(均不在y轴上)关于x轴对称,则( )A、 B、 C、 D、6. 设P为函数的图象上一点,O为坐标原点,则的最小值为( )A、2 B、 C、 D、7. , , , 则( )A、 B、 C、 D、8. 函数的图象可能是( )A、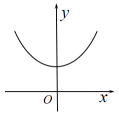 B、
B、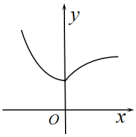 C、
C、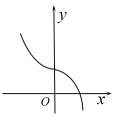 D、
D、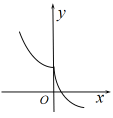
二、多选题
-
9. 设 , 则( )A、 B、 C、 D、10. 下图是某厂实施“节能减碳”措施前后,总产量y与时间x(月)的函数图象,则该厂( )
 A、前3个月的月产量逐月增加 B、第5月的月产量比第4个月少 C、第6月的月产量与第5个月持平 D、第3个月结束后开始减产,直至停产11. 已知且.下列选项中,满足为定值(与a,x的取值均无关)的是( )A、 , B、 , C、 , D、 ,12. 已知函数的图象在区间上是一条连续不断的曲线,则下列结论正确的是( )A、若 , 则在内至少有一个零点 B、若 , 则在内没有零点 C、若在内没有零点,则必有 D、若在内有唯一零点, , 则在上是单调函数
A、前3个月的月产量逐月增加 B、第5月的月产量比第4个月少 C、第6月的月产量与第5个月持平 D、第3个月结束后开始减产,直至停产11. 已知且.下列选项中,满足为定值(与a,x的取值均无关)的是( )A、 , B、 , C、 , D、 ,12. 已知函数的图象在区间上是一条连续不断的曲线,则下列结论正确的是( )A、若 , 则在内至少有一个零点 B、若 , 则在内没有零点 C、若在内没有零点,则必有 D、若在内有唯一零点, , 则在上是单调函数三、填空题
-
13. 的值为.14. 写出一个同时具有下列性质①②的函数.(注:不是常数函数)
①;②.
15. 若正数a,b满足 , 则的最大值为.16. 某工厂生产的产品中有正品和次品,其中正品重/个,次品重/个.现有10袋产品(每袋装100个),其中1袋装的全为次品,其余9袋装的全为正品.将这10袋产品从1~10编号,从第i号袋中取出i个产品 , 则共抽出个产品;将取出的产品一起称重,称出其重量 , 则次品袋的编号为.四、解答题
-
17. 已知集合 , .(1)、若 , 求;(2)、若“”是“”的充分不必要条件,求实数a的取值范围.18. 已知函数的图象时两条相邻对称轴之间的距离为 , 将的图象向右平移个单位后,所得函数的图象关于y轴对称.(1)、求函数的解析式;(2)、若 , 求的值.19. 设函数.(1)、若函数的图象C过点 , 直线与图象C交于A,B两点,且 , 求a,b;(2)、当 , 时,根据定义证明函数在区间上单调递增.20. 为宣传2022年北京冬奥会,某公益广告公司拟在一张矩形海报纸(记为矩形 , 如图)上设计三个等高的宣传栏(栏面分别为一个等腰三角形和两个全等的直角梯形),宣传栏(图中阴影部分)的面积之和为.为了美观,要求海报上所有水平方向和竖直方向的留空宽度均为.设直角梯形的高为.
 (1)、当时,求海报纸的面积;(2)、为节约成本,应如何选择海报纸的尺寸,可使用纸量最少(即矩形的面积最小)?
(1)、当时,求海报纸的面积;(2)、为节约成本,应如何选择海报纸的尺寸,可使用纸量最少(即矩形的面积最小)?