湖南省娄底市新化县2021-2022学年高一上学期数学期末考试试卷

试卷更新日期：2022-10-21 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {4 ， 5 ， 6 ， 8}$ ， $B = {3 ， 5 ， 7 ， 8}$ ，则 $A ∩ B =$ （）

A、 ${5 ， 8}$ B、 ${5 ， 6}$ C、 ${3 ， 6 ， 8}$ D、 ${3 ， 4 ， 5 ， 6 ， 7 ， 8}$

查看试题解析
2. “两个三角形相似”是“两个三角形三边成比例”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
3. 已知a，b，c，d均为实数，则下列命题正确的是（）

A、若 $a > b$ ， $c < d$ ，则 $a - c < b - d$ B、若 $a > b > 0$ ， $c < d < 0$ ，则 $a c < b d$ C、若 $a > b > 0$ ，则 $\frac{1}{a^{2}} > \frac{1}{b^{2}}$ D、若 $a > b > c > 0$ ，则 $\frac{c}{a} > \frac{c}{b}$

查看试题解析
4. 设 $a = l o g_{2} 0.3$ ， $b = 0 . 8^{e}$ ， $c = e^{0.8}$ 则a，b，c的大小关系是（）

A、 $a > b > c$ B、 $c > a > b$ C、 $c > b > a$ D、 $b > c > a$

查看试题解析
5. $\frac{1 - t a n 1 5^{∘}}{1 + t a n 1 5^{∘}}$ 的值为（）

A、 $1$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
6. 下列四个函数中，以π为最小正周期，且在区间 $(\frac{π}{2} ， π)$ 上单调递减的是（）

A、 $y = s i n x$ B、 $y = | s i n x |$ C、 $y = c o s x$ D、 $y = t a n x$

查看试题解析
7. 若函数 $f (x)$ 是定义域为 $R$ 的奇函数，且当 $x \geq 0$ 时， $f (x) = x (1 + x)$ ，则当 $x < 0$ 时， $f (x) =$ （）

A、 $- x (1 + x)$ B、 $- x (1 - x)$ C、 $x (1 + x)$ D、 $x (1 - x)$

查看试题解析
8. 酒驾是严重危害交通安全的违法行为.为了保障交通安全，根据国家有关规定： $100 m L$ 血液中酒精含量达到 $20 ~ 79 m g$ 的驾驶员即为酒后驾车， $80 m g$ 及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后，其血液中酒精含量上升到 $1 m g / m L$ .如果在停止喝酒以后，他血液中酒精含量会以每小时30%的速度减少，那么他至少要经过（）小时才能驾驶.（参考数据： $l g 2 \approx 0.3$ ， $l g 7 \approx 0.85$ ）

A、1 B、3 C、5 D、7

查看试题解析

二、多选题

9. 下列命题是真命题的是（）

A、所有的素数都是奇数 B、有一个实数x，使 $x^{2} + 2 x + 3 = 0$ C、命题“ $\forall x \in R$ ， $x + | x | \geq 0$ ”的否定是“ $\exists x \in R$ ， $x + | x | < 0$ ” D、命题“ $\exists x \in R$ ， $x + 2 \leq 0$ ”的否定是“ $\forall x \in R$ ， $x + 2 > 0$ ”

查看试题解析
10. 下列结论正确的是（）

A、 $- \frac{π}{3}$ 是第三象限角 B、若角 $α$ 的终边过点 $P (- 3 ， 4)$ ，则 $c o s α = - \frac{3}{5}$ C、若角 $α$ 为锐角，那么 $2 α$ 是第一或第二象限角 D、若圆心角为 $\frac{π}{3}$ 的扇形的弧长为 $π$ ，则该扇形面积为 $\frac{3 π}{2}$

查看试题解析
11. 设函数 $f (x) = \sin (2 x + \frac{π}{4}) + \cos (2 x + \frac{π}{4})$ ，则 $f (x)$ （）

A、是偶函数 B、在 $(0 ， \frac{π}{2})$ 单调递减 C、最大值为2 D、其图像关于直线 $x = \frac{π}{2}$ 对称

查看试题解析
12. 已知 $a \in Z$ ，关于x的一元二次不等式x²-8x+a≤0的解集中有且仅有3个整数，则a的值可以是（）

A、13 B、14 C、15 D、17

查看试题解析

三、填空题

13. $l g \sqrt[5]{100} =$ .

查看试题解析
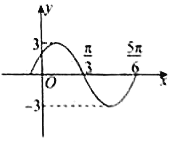
14. 已知幂函数 $y = f (x)$ 图像过点 $(2 ， \sqrt{2})$ ，则该幂函数的解析式是

查看试题解析
15. 若函数 $y = 3 s i n (ω x + φ) (ω > 0 ， 0 \leq φ < 2 π)$ 的部分图象如图所示，则此函数的解析式为.

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} 3 x^{2} + 2 (a - 1) x + 15 ， x \leq 1 \\ - 4 a + a \ln x ， x > 1 \end{array}$ ，若对任意的 $x_{1}$ 、 $x_{2} \in R$ ， $x_{1} \neq x_{2}$ ，都有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ 成立，则实数 $a$ 的取值范围是.

查看试题解析

四、解答题

17. 已知函数 $f (x) = \sqrt{x + 3} + \frac{1}{x + 2}$ .

(1)、求 $f (x)$ 的定义域和 $f (- 3)$ 的值；

(2)、当 $a > 0$ 时，求 $f (a)$ ， $f (a - 1)$ 的值.

查看试题解析
18. 已知 $α \in (0 ， \frac{π}{2})$ ， $β \in (0 ， \frac{π}{2})$ ， $c o s (α + β) = - \frac{1}{3}$ ， $t a n α = 4 \sqrt{3}$ ，求 $c o s β$ .

查看试题解析
19. 已知函数 $f (x) = \ln (2 x^{2} + a x + 3)$ .

(1)、若 $f (x)$ 是定义在R上的偶函数，求a的值及 $f (x)$ 的值域；

(2)、若 $f (x)$ 在区间 $[- 3 ， 1]$ 上是减函数，求a的取值范围.

查看试题解析
20. 已知函数 $f (x) = \sqrt{2} s i n (2 ω x - \frac{π}{4}) (ω > 0)$ 的图象的对称中心到对称轴的最小距离为 $\frac{π}{4}$ .

(1)、求函数 $f (x)$ 的解析式，并写出 $f (x)$ 的单调区间；

(2)、求函数 $f (x)$ 在区间 $[\frac{π}{8} ， \frac{3 π}{4}]$ 上的最小值和最大值以及相对应的x值.

查看试题解析
21. 物联网（InternetofThings，缩写：IOT）是基于互联网､传统电信网等信息承载体，让所有能行使独立功能的普通物体实现互联互通的网络.其应用领域主要包括运输和物流､工业制造､健康医疗､智能环境（家庭､办公､工厂）等，具有十分广阔的市场前景.现有一家物流公司计划租地建造仓库储存货物，经过市场调查了解到下列信息：仓库每月土地占地费 $y_{1}$ （单位：万元），仓库到车站的距离x（单位：千米， $x > 0$ ），其中 $y_{1}$ 与 $x + 1$ 成反比，每月库存货物费 $y_{2}$ （单位：万元）与x成正比；若在距离车站9千米处建仓库，则 $y_{1}$ 和 $y_{2}$ 分别为2万元和7.2万元.

(1)、求出 $y_{1}$ 与 $y_{2}$ 的解析式；

(2)、这家公司应该把仓库建在距离车站多少千米处，才能使两项费用之和最小？最小费用是多少？

查看试题解析
22. 已知实数 $a > 0$ ，定义域为 $R$ 的函数 $f (x) = \frac{e^{x}}{a} + \frac{a}{e^{x}}$ 是偶函数，其中 $e$ 为自然对数的底数．

(1)、求实数 $a$ 值；

(2)、判断该函数 $f (x)$ 在 $(0 ， + \infty)$ 上的单调性并用定义证明；

(3)、是否存在实数 $m$ ，使得对任意的 $t \in R$ ，不等式 $f (t - 2) < f (2 t - m)$ 恒成立．若存在，求出实数 $m$ 的取值范围；若不存在，请说明理由．

查看试题解析