河北省石家庄市2021-2022学年高一上学期数学期末考试试卷
试卷更新日期:2022-10-21 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 若幂函数的图象经过点 , 则=( )A、 B、 C、3 D、93. 祖暅原理也称祖氏原理,一个涉及几何求积的著名命题.内容为:“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高.意思是两个等高的几何体,如在等高处的截面积相等,体积相等.设A,B为两个等高的几何体,p:A、B的体积相等,q:A、B在同一高处的截面积相等.根据祖暅原理可知,p是q的( )A、充分必要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件4. 函数 的图象大致为( )A、
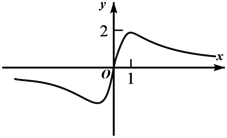 B、
B、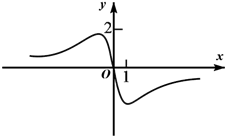 C、
C、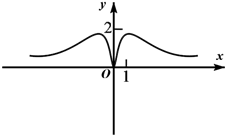 D、
D、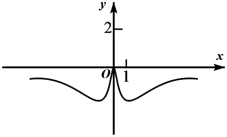 5. 设 , ,则( )A、 且 B、 且 C、 且 D、 且6. 某食品的保鲜时间(单位:小时)与储存温度(单位:)满足函数关系(为自然对数的底数,为常数)若该食品在的保鲜时间是384小时,在的保鲜时间是24小时,则该食品在的保险时间是( )小时A、6 B、12 C、18 D、247. 黄金分割比例广泛存在于许多艺术作品中.在三角形中,底与腰之比为黄金分割比的三角形被称作黄金三角形,被认为是最美的三角形,它是两底角为72°的等腰三角形.达·芬奇的名作《蒙娜丽莎》中,在整个画面里形成了一个黄金三角形.如图,在黄金三角形中, , 根据这些信息,可得( )
5. 设 , ,则( )A、 且 B、 且 C、 且 D、 且6. 某食品的保鲜时间(单位:小时)与储存温度(单位:)满足函数关系(为自然对数的底数,为常数)若该食品在的保鲜时间是384小时,在的保鲜时间是24小时,则该食品在的保险时间是( )小时A、6 B、12 C、18 D、247. 黄金分割比例广泛存在于许多艺术作品中.在三角形中,底与腰之比为黄金分割比的三角形被称作黄金三角形,被认为是最美的三角形,它是两底角为72°的等腰三角形.达·芬奇的名作《蒙娜丽莎》中,在整个画面里形成了一个黄金三角形.如图,在黄金三角形中, , 根据这些信息,可得( ) A、 B、 C、 D、8. 已知函数 , 若存在不相等的实数a,b,c,d满足 , 则的取值范围为( )A、 B、 C、 D、
A、 B、 C、 D、8. 已知函数 , 若存在不相等的实数a,b,c,d满足 , 则的取值范围为( )A、 B、 C、 D、二、多选题
-
9. 下列结论中,正确的是( )A、函数是指数函数 B、函数的值域是 C、若 , 则 D、函数的图像必过定点10. 若 ,则下列关系式中一定成立的是( )A、 B、 ( ) C、 ( 是第一象限角) D、11. 已知函数 , , 的零点分别为a,b,c,以下说法正确的是( )A、 B、 C、 D、12. 已知定义在R上的函数的图象连续不断,若存在常数 , 使得对于任意的实数x恒成立,则称是回旋函数.给出下列四个命题中,正确的命题是( )A、函数是回旋函数 B、函数(其中a为常数,)为回旋函数的充要条件是 C、若函数为回旋函数,则 D、函数是的回旋函数,则在上至少有1011个零点
三、填空题
-
13.14. 已知某扇形的半径为 , 面积为 , 那么该扇形的弧长为.15. 已知 , 且 , 则16. 设函数(e为自然对数的底数,a为常数),若为偶函数,则实数;若对 , 恒成立,则实数a的取值范围是
四、解答题
-
17. 在非空集合① , ② , ③这三个条件中任选一个,补充在下面问题中,已知集合__________,
使“”是“”的充分不必要条件,若问题中a存在,求a的值;若a不存在,请说明理由.(如果选择多个条件分别解答,按第一个解答计分).
18. 已知 .(1)、求 的值(2)、求 的值.19. 已知函数 .(1)、若 , 求不等式的解集;(2)、若 , 且 , 求的最小值.20. 已知函数(1)、求函数的最小正周期和单调递减区间;(2)、将函数的图像向左平移单位长度,再将所得图像上各点的横坐标缩短为原来的 , 纵坐标不变,得到函数的图像,求在上的值域.21. 已知函数 是定义在 上的奇函数,且 .(1)、求函数 的解析式;(2)、判断函数 在 上的单调性,并用定义证明;(3)、解关于 的不等式, .22. 某自然资源探险组织试图穿越某峡谷,但峡谷内被某致命昆虫所侵扰,为了穿越这个峡谷,该探险组织进行了详细的调研,若每平方米的昆虫数量记为昆虫密度 , 调研发现,在这个峡谷中,昆虫密度是时间(单位:小时)的一个连续不间断的函数其函数表达式为,
其中时间是午夜零点后的小时数,为常数.
(1)、求的值;(2)、求出昆虫密度的最小值和出现最小值的时间;(3)、若昆虫密度不超过1250只/平方米,则昆虫的侵扰是非致命性的,那么在一天24小时内哪些时间段,峡谷内昆虫出现非致命性的侵扰.