(北师大版)2022-2023学年度第一学期八年级数学7.5 三角形的内角和定理 同步测试
试卷更新日期:2022-10-21 类型:同步测试
一、单选题
-
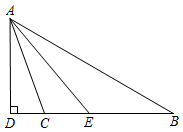
1. 如图,在△ABC中,AD平分∠BAC,点E在射线BC上,EF⊥AD于F,∠B=40°,∠ACE=72°,则∠E的度数为( )
 A、68° B、56° C、34° D、32°2. 如图,线段、相交于点 , 连接、 , 和的平分线和相交于点 , 则与、之间存在的数量关系为( )
A、68° B、56° C、34° D、32°2. 如图,线段、相交于点 , 连接、 , 和的平分线和相交于点 , 则与、之间存在的数量关系为( ) A、 B、 C、 D、3. 如图,直角三角形纸片ABC中,∠ACB=90°,∠A=50°,将其沿边AB上的中线CE折叠,使点A落在点 处,则∠ EB的度数为( )
A、 B、 C、 D、3. 如图,直角三角形纸片ABC中,∠ACB=90°,∠A=50°,将其沿边AB上的中线CE折叠,使点A落在点 处,则∠ EB的度数为( )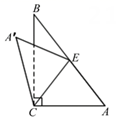 A、10° B、15° C、20° D、40°4. 如图,在等腰中, , , 的平分线与AB的垂直平分线交于点E,沿FG折叠使点C与点E重合,则的度数是( ).
A、10° B、15° C、20° D、40°4. 如图,在等腰中, , , 的平分线与AB的垂直平分线交于点E,沿FG折叠使点C与点E重合,则的度数是( ). A、60度 B、55° C、50° D、45°5. 如图,在和中, , , , 则( )
A、60度 B、55° C、50° D、45°5. 如图,在和中, , , , 则( )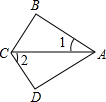 A、30° B、40° C、50° D、60°6. 等腰三角形的顶角为80°,则其底角的度数是( )A、100° B、80° C、50° D、40°7. 如图,将的BC边对折,使点B与点C重合,DE为折痕,若 , , 则( ).
A、30° B、40° C、50° D、60°6. 等腰三角形的顶角为80°,则其底角的度数是( )A、100° B、80° C、50° D、40°7. 如图,将的BC边对折,使点B与点C重合,DE为折痕,若 , , 则( ). A、45° B、60° C、35° D、40°8. 一个三角形三个内角之比为1:3 :5,则最小的角的度数为( )A、20° B、30° C、40° D、60°9. 如图,在△ABC中,∠B = 46°,∠ADE =40°,AD平分∠BAC 交BC于D,DE∥AB,交AC于E,则∠C 的大小是( )
A、45° B、60° C、35° D、40°8. 一个三角形三个内角之比为1:3 :5,则最小的角的度数为( )A、20° B、30° C、40° D、60°9. 如图,在△ABC中,∠B = 46°,∠ADE =40°,AD平分∠BAC 交BC于D,DE∥AB,交AC于E,则∠C 的大小是( ) A、46° B、54° C、66° D、80°10. 已知, , , 的相关数据如图所示,则下列选项正确的是( )
A、46° B、54° C、66° D、80°10. 已知, , , 的相关数据如图所示,则下列选项正确的是( )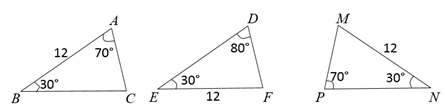 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图所示,和是分别沿着 , 边翻折形成的,若:::: , 则的度数为 .
 12. 如图△ABC中,AD⊥BC于点D,AE平分∠CAD交BC于E,若∠C= 60°,则∠DEA= .
12. 如图△ABC中,AD⊥BC于点D,AE平分∠CAD交BC于E,若∠C= 60°,则∠DEA= . 13. 如图,将长方形纸片ABCD沿AE折叠,使点D落在BC边上的F处,如果∠AEF =75°,那么∠BAF =°.
13. 如图,将长方形纸片ABCD沿AE折叠,使点D落在BC边上的F处,如果∠AEF =75°,那么∠BAF =°.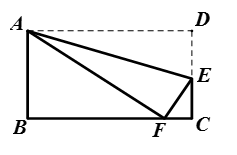 14. 如图,将纸片沿折叠,使点落在点处,且平分 , 平分 , 若 , 则的度数为.
14. 如图,将纸片沿折叠,使点落在点处,且平分 , 平分 , 若 , 则的度数为. 15. 如图,已知∠BAC=130°,AB=AC,AC的垂直平分线交BC于点D,则∠BAD=;
15. 如图,已知∠BAC=130°,AB=AC,AC的垂直平分线交BC于点D,则∠BAD=;
三、解答题
-
16. 如图所示,点E在 外部,点D在BC边上,DE交AC于F,若 ,AD=AB,求证:AC=AE.
 17. 如图,点D是△ABC的边BC上一点,AB=AC=CD , ∠BAC=100°,求∠BAD的度数.
17. 如图,点D是△ABC的边BC上一点,AB=AC=CD , ∠BAC=100°,求∠BAD的度数. 18. 如图,在△ABC中,AB=AC , 点D在AC上,且BD=BC=AD , 求∠A的度数.
18. 如图,在△ABC中,AB=AC , 点D在AC上,且BD=BC=AD , 求∠A的度数. 19. 如图, , ,点D在AC边上, ,AE和BD相交于点O.若 ,求 的度数.
19. 如图, , ,点D在AC边上, ,AE和BD相交于点O.若 ,求 的度数. 20. 如图,在△ABC 中,∠ABC=60°,∠ACB=82°,延长CB至D , 使DB=BA , 延长BC至E , 使CE=CA , 连接AD , AE . 求∠D , ∠E , ∠DAE 的度数.
20. 如图,在△ABC 中,∠ABC=60°,∠ACB=82°,延长CB至D , 使DB=BA , 延长BC至E , 使CE=CA , 连接AD , AE . 求∠D , ∠E , ∠DAE 的度数. 21. 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.
21. 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.