（北师大版）2022-2023学年度第一学期八年级数学7.4 平行线的性质 同步测试
试卷更新日期：2022-10-21 类型：同步测试
一、单选题
-
1. 如图， ， 若 ， 则的度数是（ ）
A、 B、 C、 D、2. 已知：如图，直线a，b被直线c所截，且a∥b，若∠2＝110°，则∠1的度数是（ ）
A、130° B、110° C、80° D、70°3. 如图，把一张长方形纸片沿折叠后，点落在边上的点处，点落在点处，若 ， 则图中的度数为（ ）
A、 B、 C、 D、4. 如图，ABEF，∠C＝90°，则α、β、γ的关系是（ ）
A、＋－＝90° B、＋＋＝180° C、＋－＝90° D、＝＋5. 一把直尺与一块直角三角板按下图方式摆放，若 ， 则（ ）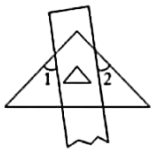
A、52° B、53° C、54° D、63°6. 如图，BD是的角平分线， ， 交AB于点E．若 ， ， 则的度数是（ ）
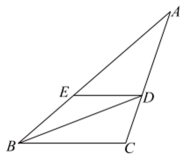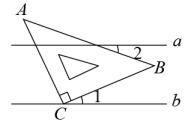
A、10° B、20° C、30° D、50°7. 生活中常见的探照灯、汽车大灯等灯具都与抛物线有关．如图，从光源P点照射到抛物线上的光线等反射以后沿着与直线平行的方向射出，若 ， ， 则的度数为（ ）°
A、 B、 C、 D、8. 如图，直线a∥b，将含有45°的三角板ABC的直角顶点C放在直线b上，若∠1＝25°，则∠2的度数是（ ）
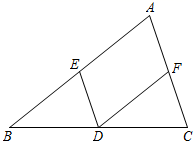
A、10° B、15° C、25° D、20°9. 如图，直线a∥b，直角三角板ABC的直角顶点C在直线b上，若∠1＝55°，则∠2＝（ ）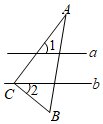
A、55° B、45° C、35° D、25°10. 如图，AF是∠BAC的平分线， DF∥AC，若∠1＝25°，则∠BDF的度数为（ ）
A、25° B、50° C、75° D、100°二、填空题
-
11. 如图，将长方形纸片沿CB，CD折叠成图1，使MC，FC在同一直线上，FC交BD于点G，再沿GD折叠成图2，使点E落在点E′处，点F落在点F′处，点C位于四边形DGF′E′的内部，GF′交CB于点H，若∠CDE′＝21°，则∠CBG的度数为 °.
12. 如图，有一条直的宽纸带，按图折叠，已知∠1＝26°，则∠2＝度．
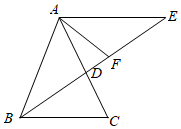
13. 将一把直尺与含30°的直角三角板如图摆放，使三角板的一个锐角顶点落在直尺的一边上，若∠1＝40°，则∠2＝°．
14. 如图， ， 若 ， ， ， 则∠AEC的度数为 ．
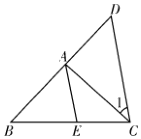15. 如图，在△ABC中，点D、E分别为边BC、AC上的点，将△CDE沿DE翻折得到△C′DE，使C′D∥AB．若∠A＝75°，则∠C′EA的大小为 °．
三、解答题
-
16. 如图，AB∥CD，连接BC，若BD平分∠ABC，∠D＝50°．求∠C的度数．
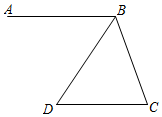17. 如图，在四边形ABCD中，AB∥CD，∠ADC=90°，E在AC上．EC＝ED＝DA．求∠CAB的度数．
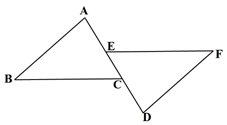
18. 如图，已知DE∥BC，BE是∠ABC的平分线，∠C=70°，∠ABC=50°．求∠DEB和∠BEC的度数．
19. 已知：如图，在△ADF和△BCE中，点B，F，E，D依次在一条直线上，若AF∥CE，∠B ∠D ，BF DE，求证：AF CE．
20. 如图，ABCF，E为DF的中点，AB=20，CF=15，求BD的长度.
