(北师大版)2022-2023学年度第一学期八年级数学7.2 定义与命题 同步测试
试卷更新日期:2022-10-21 类型:同步测试
一、单选题
-
1. 下列命题:(1)无限循环小数是无理数;(2)绝对值等于它本身的数是非负数;(3)垂直于同一直线的两条直线互相平行;(4)有两边和其中一边的对角对应相等的两个三角形全等;(5)面积相等的两个三角形全等,是假命题的有( )A、1个 B、2个 C、3个 D、4个2. 下列语句正确的有( )个.
①“相等的角是对顶角”是真命题;②“同角(或等角)的补角相等”是真命题;③立方根等于它本身的数是非负数;④如果一个等腰三角形的两边长分别是2cm和5m,则周长是9cm或12cm.
A、4 B、3 C、2 D、13. 数学中说明某个命题不成立时常采用“举反例”,即举一个满足条件,但不满足结论的例子.为说明命题“对于任何实数a,都有 =a”是假命题,所列举反例正确的是( )A、a=﹣2 B、a= C、a=1 D、a=4. 下列命题是真命题的是( )A、同旁内角互补 B、任意一个等腰三角形一定是钝角三角形 C、两边及一角对应相等的两个三角形全等 D、角平分线上的点到角两边的距离相等5. 能说明命题“对于任意实数a,都有a2>0”是假命题的反例是( )A、a=﹣2 B、a=1 C、a=0 D、a=6. 对于命题“若a>b,则a2>b2”,小明想举一个反例说明它是一个假命题,则符合要求的反例可以是( )A、a=﹣1,b=0 B、a=2,b=﹣1 C、a=2,b=1 D、a=﹣1,b=﹣27. 下列说法错误的是( )A、16的算术平方根是4 B、三角形的一个外角等于任意两个内角之和 C、一次函数y=﹣2x+3的图象不经过第三象限 D、在平面直角坐标系中,若一个点的坐标为(3,0),则这个点在x轴上8. 下列命题中:①相等的角是对顶角;②如果 , 那么;③两边分别相等且其中一组等边的对角相等的两个三角形全等;④三角形的内角和等于180°.其中是真命题的个数为( )A、0个 B、1个 C、2个 D、3个9. 下列命题错误的个数有( )①实数与数轴上的点一一对应;②无限小数就是无理数;③三角形的一个外角大于任何一个和它不相邻的内角;④两条直线被第三条直线所截,同旁内角互补.
A、1个 B、2个 C、3个 D、4个10. 下列命题是假命题的是( ).A、是最简二次根式 B、若点A(-2,a),B(3,b)在直线y=-2x+1,则a>b C、数轴上的点与有理数一一对应 D、点A(2,5)关于y轴的对称点的坐标是(-2,5)二、填空题
-
11. 给出下列语句:①延长线段AB到点C;②垂线段最短;③过点A画直线EF;④在△ABC中,若AB>AC,则∠B>∠C.其中是命题的有(只填序号).12. 命题“两个全等三角形的周长相等”的逆命题是.13. 有下列命题:①可以在数轴上表示无理数;②若 , 则;③无理数的相反数还是无理数.其中是真命题的为(填序号).14. 命题“垂直于同一直线的两条直线互相垂直”是命题.(填“真”或“假”)15. 命题“a<2a”是 命题(填“真”或“假”).
三、解答题
-
16. 证明:等腰三角形两腰上的中线相等17. 证明命题“等腰三角形两腰上的中线相等”。(自己画出图形)
已知:
求证:
证明:
18. 下列命题中,哪些是真命题?哪些是假命题?①内错角相等;
②两直线平行,同旁内角互补;
③若x=2,则x+1>1;
④不等式两边同时乘以或除以一个负数,不等号应改变方向;
⑤三角形两边之和大于第三边.
19. 如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截.在下面三个条件中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.①AB⊥BC,CD⊥BC,②BE∥CF,③∠1=∠2.
 20. “定义、定理、基本事实、命题、真命题、假命题”它们之间的关系恰好可以用下图表示,请指出A,B,C,D,E,F分别与它们中的哪一个对应.
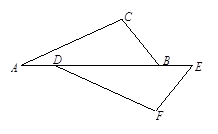
20. “定义、定理、基本事实、命题、真命题、假命题”它们之间的关系恰好可以用下图表示,请指出A,B,C,D,E,F分别与它们中的哪一个对应. 21. 已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE, ∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.
21. 已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE, ∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.