（北师大版）2022-2023学年度第一学期八年级数学第六章数据的分析同步测试

试卷更新日期：2022-10-20 类型：单元试卷

进入出卷网下载

一、单选题

1. 在一次“爱心捐助”捐款活动中，某班第一小组8名同学捐款的金额(单位：元）如表所示，则这 $8$ 名同学捐款的平均金额为（）

金额/元

5

6

7

10

人数

2

3

2

1

A、6.5元 B、6元 C、3.5元 D、7元

查看试题解析
2. 某天上午8：00小李从家中出发，以2米/秒的速度于8：15到了商店，然后以2.5米/秒的速度于8：20到达书店，则小李从家到书店的平均速度为（）

A、2.25 B、2.125 C、2.175 D、2.225

查看试题解析
3. 某校举行“喜迎中国共产党建党100周年”党史知识竞赛，下表是10名决赛选手的成绩．这10名决赛选手成绩的众数是（）
分数
100
95
90
85
人数
1
4
3
2

A、85 B、90 C、95 D、100

查看试题解析
4. 抢微信红包成为节日期间人们最喜欢的活动之一．对某单位50名员工在春节期间所抢的红包金额进行统计，并绘制成了统计图．根据如图提供的信息，红包金额的众数和中位数分别是（）

A、20，20 B、30，20 C、30，30 D、20，30

查看试题解析
5. 已知一组数据：2，0， $- 1$ ，4，2， $- 3$ ．这组数据的众数和中位数分别是（）

A、2，1.5 B、2，-1 C、2，1 D、2，2

查看试题解析
6. 如果你和其余6人进入了八年级速算比赛的总决赛，你想知道自己是否能进入前3名，只需要了解自己的成绩以及全部成绩的（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
7. 小明收集了鄂尔多斯市某酒店2021年3月1日～3月6日每天的用水量（单位：吨），整理并绘制成如图所示的折线统计图，下列结论正确的是（）

A、平均数是 $\frac{23}{4}$ B、众数是10 C、中位数是8.5 D、方差是 $\frac{25}{3}$

查看试题解析
8. 已知数据1，2，3，3，4，5，则下列关于这组数据的说法错误的是（　　）

A、平均数、中位数和众数都是3 B、极差为4 C、方差是 $\frac{5}{3}$ D、标准差是 $\sqrt{10}$

查看试题解析
9. 甲、乙、丙、丁四位同学都参加了5次数学模拟测试，每个人这5次成绩的平均数都是92分，方差分别是 $S_{甲}^{2} = 0.85$ ， $S_{乙}^{2} = 0.72$ ， $S_{丙}^{2} = 0.63$ ， $S_{丁}^{2} = 0.35$ ，则这5次测试成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
10. 甲、乙、丙、丁四名同学进行立定跳远测试，每人10次立定跳远成绩的平均数都是2.25米，方差分别是 $S_{甲}^{2} = 0.72$ ， $S_{乙}^{2} = 0.75$ ， $S_{丙}^{2} = 0.68$ ， $S_{丁}^{2} = 0.61$ ，则这四名同学立定跳远成绩最稳定的是（）．

A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题

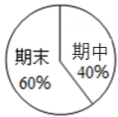
11. 小明八年级上学期数学期中成绩是110分，期末是115分，若学期的总评成绩是根据如图的权重计算，则小明该学期的数学总评成绩为分．

查看试题解析
12. 小明所在班级为希望工程捐款，他统计了全班同学的捐款情况，并绘制成如图所示的统计图，根据统计图，可计算出全班同学平均每人捐款元．

查看试题解析
13. 一组数据2，3，x，y，12中，唯一的众数是12，平均数是6，这组数据的中位数是.

查看试题解析
14. 若多项式5x²＋17x﹣12可因式分解成（x＋a）（bx＋c），其中a、b、c均为整数，则a，b，c的中位数是

查看试题解析
15. 甲、乙、丙三位同学参加演讲比赛，经过三轮比赛后，三人的成绩平均分相同，方差分别是S甲²＝1.2，S乙²＝3.3，S丙²＝1.5．你认为成绩比较稳定的是（填“甲”或“乙”或“丙”）．

查看试题解析

三、解答题

16. 某公司欲招聘一名公关人员，对甲、乙两位候选人进行了笔试和面试，他们的成绩如表所示：
候选人
测试成绩（百分制）
笔试
面试
甲
95
85
乙
83
95
根据需要，笔试与面试的成绩按4：6的比例确定个人成绩（成绩高者被录用），那么谁将被录用？

查看试题解析
17. 下表是某班5名同学某次数学测试成绩．根据信息完成下表，并回答问题．五人中分数最高的是谁？分数最低的是谁？谁的分数与全班平均分最接近？
姓名
王芳
刘兵
张昕
李聪
江文
成绩
89

84

与全班平
均分之差
﹣1
+2
0

﹣2

查看试题解析

18. 甲、乙两人在

5

次打靶测试中命中的环数如下：

	第一次	第二次	第三次	第四次	第五次
甲	$8$	$8$	$7$	$8$	$9$
乙	$6$	$9$	$7$	$9$	$9$

从数据来看，谁的成绩较稳定？请你通过计算方差说明理由.

查看试题解析

19. 为了考察甲、乙两种成熟期小麦的株高长势状况，现从中各随机抽取6株，并测得它们的株高（单位：cm）如下表所示：

甲

63

66

63

61

64

61

乙

63

65

60

63

64

63

请分别计算表内两组数据的方差，并借此比较哪种小麦的株高长势比较整齐.

查看试题解析

四、综合题

20. 某校开展了以“不忘初心，奋斗新时代”为主题的读书活动，校德育处对本校八年级学生九月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了抽样调查，随机抽取八年级部分学生，对他们的“读书量”（单位：本）进行了统计，并将统计结果绘制成了如下统计图：

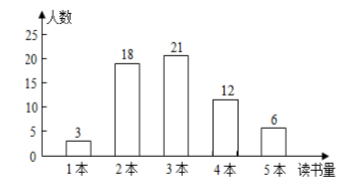(1)、本次所抽取学生九月份“读书量”的众数为本，中位数为本；

(2)、求本次所抽取学生九月份“读书量”的平均数.

查看试题解析

21. 某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的满分均为100分，前6名选手的得分如下：

序号	1号	2号	3号	4号	5号
笔试成绩/分	85	92	84	90	84
面试成绩/分	90	88	86	90	80

根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩．

(1)、这6名选手笔试成绩的众数是分．

(2)、现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比．

(3)、求出其余五名选手的综合成绩，并以综合成绩排序确定前两名人选．