（北师大版）2022-2023学年度第一学期八年级数学6.4 数据的离散程度 同步测试
试卷更新日期：2022-10-20 类型：同步测试
一、单选题
-
1. 甲、乙两名运动员在相同的条件下，各射击10次，经过计算，甲、乙两人成绩的平均数均是9.5环，甲的成绩的方差是0.125，乙的成绩的方差是1.85，那么这10次射击中，甲、乙成绩的稳定情况是（ ）A、甲较为稳定 B、乙较为稳定 C、两个人成绩一样稳定 D、不能确定2. 甲、乙、丙、丁四个旅游团的游客人数都相等，且每个旅游团游客的平均年龄都是35岁，这四个旅游团游客年龄的方差分别为S甲2＝6，S乙2＝1.8，S丙2＝5，S丁2＝8，这四个旅游团中年龄相近的旅游团是（ ）A、甲团 B、乙团 C、丙团 D、丁团3. 某校八年级进行了三次数学测试，甲、乙、丙、丁4名同学三次数学成绩的平均分都是109分，方差分别是 ， 则这4名同学三次数学成绩最稳定的是（ ）A、甲 B、乙 C、丙 D、丁4. 某校八年级人数相等的甲、乙、丙三个班，同时参加了一次数学测试，对成绩进行了统计分析，平均分都是72分，方差分别为 ， ， ， 则成绩波动最小的班级（ ）A、甲 B、乙 C、丙 D、无法确定5. 班级准备推选一名同学参加学校演讲比赛，在五轮班级预选赛中，甲、乙、丙三名同学五轮预选赛成绩的平均数和方差如下表所示：
甲
乙
丙
平均数/分
96
95
97
方差
0.4
2
2
丁同学五轮预选赛的成绩依次为：97分、96分、98分、97分、97分，根据表中数据，要从甲、乙、丙、丁四名同学中选择一名成绩好又发挥稳定的同学参赛应该选择（ ）
A、甲 B、乙 C、丙 D、丁6. 在一次数学测试中，某小组五名同学的成绩（单位：分）如下表（有两个数据被遮盖）．组员
甲
乙
丙
丁
戊
方差
平均成绩
得分
81
79
80
82
80
那么被遮盖的两个数据依次是（ ）
A、80，2 B、80，10 C、78，2 D、78，107. 一组数据a、b、c、d、e、f、g的平均数是m ， 方差是n ， 则另一组数据2a-3、2b-3、2c-3、2d-3、2e-3、2f-3、2g-3的平均数和方差分别是（ ）A、2m、 B、 、n C、 、2n D、 、4n8. 为研究甲、乙、丙、丁四种杂交水稻的长势，某研究所分别从四亩试验田中抽取20株测其高度进行统计分析，结果如下：S甲2＝0.9米2、S乙2＝1.5米2 ， S丙2＝2.3米2 ， S丁2＝3.2米2 ， 则四种杂交水稻中长势比较整齐的是（ ）A、甲 B、乙 C、丙 D、丁9. 用计算器计算方差时，要首先进入统计计算状态，需要按键（ ）A、
B、
C、
D、
10. 如果样本方差S2= [(x1-2)2+(x2-2)2+(x3-2)2+(x4-2)2+(x5-2)2]，则样本和x1+x2+x3+x4+x5= （ ）A、10 B、4 C、5 D、2二、填空题
-
11. 用 计算一组数据的方差，那么x1+x2+x3…+x8＝.12. 某班甲、乙两个同学在5次模拟测试中，数学的平均成绩都是142分，方差分别是 ， .在甲、乙两人中，成绩较稳定的是.13. 甲、乙、丙三人进行射击测试，每人射击10次的平均成绩都是9.2环，方差分别是 ， ， ， 则三人中成绩最稳定的是（填“甲”或“乙”或“丙”）．14. 黔东南州某校今年春季开展体操活动，小聪收集、整理了成绩突出的甲、乙两队队员（各50名）的身高得到：平均身高（单位：cm）分别为：＝160， ， 方差分别为： ， ， 现要从甲、乙两队中选出身高比较整齐的一个队参加上一级的体操比赛，根据上述数据，应该选择 ．（填写“甲队”或“乙队”）15. 八年级（1）、（2）两班人数相同，在同一次数学单元测试中，班级平均分和方差如下：则成绩较为稳定的班级是.
三、解答题
-
16. 某运动队欲从甲、乙两名优秀选手中选一名参加全省射击比赛，该运动队预先对这两名选手进行了8次测试，测得的成绩如表：
次数
选手甲的成绩（环）
选手乙的成绩（环）
1
9.6
9.5
2
9.7
9.9
3
10.5
10.3
4
10.0
9.7
5
9.7
10.5
6
9.9
10.3
7
10.0
10.0
8
10.6
9.8
根据统计的测试成绩，请你运用所学过的统计知识作出判断，派哪一位选手参加比赛更好？为什么？
17. 某同学使用计算器求30个数据的平均数时，错将其中一个数据105输成了15，则由此求出的平均数与实际平均数的差是多少？18. 甲、乙两人分别在六次射击中的成绩如下表：（单位：环）第1次
第2次
第3次
第4次
第5次
第6次
甲
6
7
7
8
6
8
乙
5
9
6
8
5
9
分别算出两人射击的平均数和方差．这六次射击中成绩发挥比较稳定的是谁？
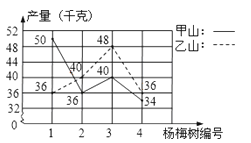
19.王大伯几年前承包了甲、乙两片荒山，各栽100棵杨梅树，成活98%．现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的杨梅，每棵的产量如折线统计图所示．
（1）分别计算甲、乙两山样本的平均数，并估算出甲、乙两山杨梅的产量总和；
（2）试通过计算说明，哪个山上的杨梅产量较稳定？
20. 甲、乙、丙、丁四支足球队在世界杯预选赛中进球数分别为9，9，x，7，若这组数据的众数和平均数恰好相等，求出其中的x值以及此组数据的标准差．21. 甲、乙两位同学本学年每个单元的测验成绩如下（单位：分）：甲：98，100，100，90，96，91，89，99，100，100，93
乙：98，99，96，94，95，92，92，98，96，99，97
（1）他们的平均成绩分别是多少？
（2）甲、乙的11次单元测验成绩的标准差分分别是多少？
（3）这两位同学的成绩各有什么特点？
（4）现要从中选出一人参加“希望杯”竞赛，历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，你认为应选谁参加这项竞赛，为什么？
22.为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看3次的人数没有标出）．
根据上述信息，解答下列各题：
（1）该班级女生人数是?女生收看“两会”新闻次数的中位数是?
（2）对于某个群体，我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”．如果该班级男生对“两会”新闻的“关注指数”比女生低5%，试求该班级男生人数；
（3）为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计量（如表）．
统计量
平均数（次）
中位数（次）
众数（次）
方差
…
该班级男生
3
3
4
2
…
根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小．
23. 我校准备挑选一名跳高运动员参加区中学生运动会，对跳高队的甲、乙两名运动员进行了8次选拔比赛，他们的成绩（单位：cm）如下：
甲：170 165 168 169 172 173 168 167
乙：160 173 172 161 162 171 170 175
（1）甲、乙两名运动员的跳高平均成绩分别是多少？
（2）哪名运动员的成绩更为稳定？为什么？
（3）若预测，跳过165cm就很可能获得冠军。该校为了获得冠军，可能选哪位运动员参赛？若预测跳过170cm才能得冠军呢？为什么？