2022年秋季北师版数学九年级上册第五章 《投影与视图》单元检测B
试卷更新日期：2022-10-20 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 如图，这是一个机械模具，则它的俯视图是（ ）
A、
B、
C、
D、
2. 小华同学的身高为1.6米，某一时刻他在阳光下的影长为2米，与他邻近的一棵树的影长为6米，则这棵树的高为（ ）A、3.2米 B、4.8米 C、5.2米 D、5.6米3. 下列四幅图中，能表示两棵树在同一时刻太阳光下的影子的图是（ ）A、
B、
C、
D、
4. 如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，他测得落在地面上影长为BD＝9.6米，留在墙上的影长CD＝2米，则旗杆的高度（ ）
A、12米 B、10.2米 C、10米 D、9.6米5. 如图，在直角坐标系中，点P(2，2)是一个光源．木杆AB两端的坐标分别为(0，1)，(3，1)．则木杆AB在x轴上的投影长为（ ）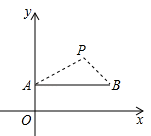
A、3 B、4 C、5 D、66. 如图，有一路灯杆AP，路灯P距地面4.8m，身高1.6m的小明站在距A点4.8m的点D处，小明的影子为DE，他沿射线DA走2.4m到达点B处，小明的影子为BC，此时小明影子的长度（ ）
A、增长了1m B、缩短了1m C、增长了1.2m D、缩短了1.2m7. 如图，小聪和他同学利用影长测量旗杆的高度，当1米长的直立的竹竿的影长为1.5米时，此时测得旗杆落在地上的影长为12米，落在墙上的影长为2米，则旗杆的实际高度为（ ）
A、8米 B、10米 C、18米 D、20米8. 如图，一直角边长为4cm的等腰直角三角板在灯光照射下形成投影，该三角板与其投影的相似比为2∶3．则投影三角形的面积为（ ）
A、36 B、18 C、16 D、209. 如图，小颖身高为 ，在阳光下影长 ，当她走到距离墙角（点 ） 的 处时，她的部分影子投射到墙上，则投射在墙上的影子 的长度为（ ）
A、 B、 C、 D、10. 某校积极开展综合实践活动，一次九年级数学小组发现校园里有一棵被强台风摧折的大树，其残留的树桩DC的影子的一端E刚好与倒地的树梢重合，于是他们马上利用其测量旁边钟楼AB的高度．如图是根据测量活动场景抽象出的平面图形．活动中测得的数据如下：
①大树被摧折倒下的部分DE＝10m；
②tan∠CDE＝ ；
③点E到钟楼底部的距离EB＝7m；
④钟楼AB的影长BF＝（20 +8）m；
⑤从D点看钟楼顶端A点的仰角为60°．
（点C ， E ， B ， F在一条直线上）．
请你选择几个需要的数据，用你喜欢的方法求钟楼AB的高度，则AB＝（ ）
A、15 m B、（15 +6）m C、（12 +6）m D、15m二、填空题（每题3分，共18分）
-
11. 如图，电线杆上的路灯距离地面 ，身高 的小明（ ）站在距离电线杆的底部（点O） 的A处，则小明的影子 长为m.
12. 小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上；如图，此时测得地面上的影长为8米，坡面上的影长为4米．已知斜坡的坡角为30°，同一时刻，一根长为1米，垂直于地面放置的标杆在地面上的影长为2米，则树的高度为 ．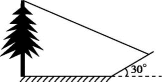
13. 如图，在同一时刻，测得小华和旗杆的影长分别为1m和6m，小华的身高约为1.6m，则旗杆的高约为m.
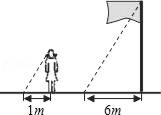14. 一幢4层楼房只有一个窗户亮着一盏灯，一棵小树和一根电线杆在窗口灯光下的影子如图所示，则亮着灯的窗口是号窗口．
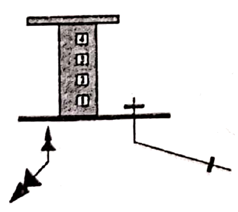15. 在数学活动课上，老师带领数学小组测量大树 的高度．如图，数学小组发现大树离教学楼有5m，高1.4m的竹竿在水平地面的影子长1m，此时大树的影子有一部分映在地面上，还有一部分映在教学楼的墙上，墙上的影子离 为2m，那么这棵大树高m．
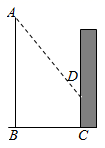16. 几个完全相同的小正方体搭成如图的几何体，从上面拿掉一个或者几个小正方体（不能直接拿掉被压在下面的小正方体）而不改变几何体的三视图的方法有种.
三、解答题（共8题，共72分）
-
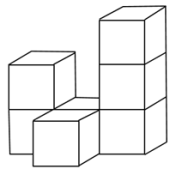
17. 如图是由7个棱长为1的小正方体搭成的几何体.
(1)、请分别画出这个几何体的左视图和俯视图；(2)、这个几何体的表面积为（包括底面积）；(3)、若使得该几何体的俯视图和左视图不变，则最多还可以放个相同的小正方体.18. 据说，在距今2500多年前，古希腊数学家就已经较准确地测出了埃及金字塔的高度，操作过程大致如下：如图所示，设AB是金字塔的高，在某一时刻，阳光照射下的金字塔在底面上投下了一个清晰的阴影，塔顶A的影子落在地面上的点C处，金字塔底部可看作方正形FGHI，测得正方形边长FG长为160米，点B在正方形的中心，BC与金字塔底部一边垂直于点K，与此同时，直立地面上的一根标杆DO留下的影子是OE，射向地面的太阳光线可看作平行线（AC∥DE），此时测得标杆DO长为1.2米，影子OE长为2.7米，KC长为250米，求金字塔的高度AB及斜坡AK的坡度（结果均保留四个有效数字）
19. 如图，路灯（P点）距地面8米，身高1.6米的小明从距离路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点（B点在A点的左边）时，身影的长度是变长了还是变短了？变长或变短了多少米？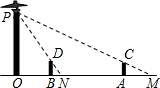
20. 某校数学社团开展“探索生活中的数学”研学活动，准备测量秦始皇雕塑的高度.如图所示，首先，在阳光下，某一时刻，小玉在雕塑影子顶端处竖立一根高2米的标杆 ， 此时测得标杆的影子为2米；然后，在处竖立一根高2.5米的标杆 ， 小婷从处沿后退0.8米到处恰好看到点、在一条直线上，小婷的眼睛到地面的距离米，米，已知 ， ， ， ， 点、、、、在同一水平直线上，请根据以上数据求出秦始皇雕塑的高度.
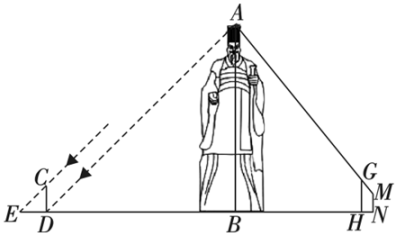21. 晚上，小亮在广场乘凉，图中线段 表示站立在广场上的小亮，线段 表示直立在广场上的灯杆，点 表示照明灯．
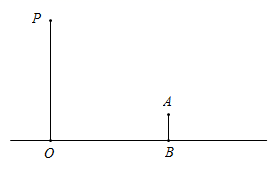(1)、请你在图中画出小亮在照明灯 照射下的影子 （请保留作图痕迹，并把影子描成粗线）；(2)、如果小亮的身高 ，测得小亮影长 ，小亮与灯杆的距离 ，请求出灯杆的高 ．22. 如图，小华在晚上由路灯A走向路灯B.当他走到点P时，发现他身后影子的顶部刚好接触到路灯A的底部；当他向前再步行12m到达点Q时，发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m，两个路灯的高度都是9.6m，且AP＝QB.
(1)、求两个路灯之间的距离；(2)、当小华走到路灯B的底部时，他在路灯A下的影长是多少？
