（北师大版）2022-2023学年度第一学期八年级数学4.4一次函数的应用同步测试

试卷更新日期：2022-10-20 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，元旦期间，某移动公司推出两种不同的收费标准：A种方式是月租20元，B种方式是月租0元，一个月本地网内打出时间t（分）与打出电话费s（元）的函数关系图象，当打出200分钟时，这两种方式的电话费相差（）

A、15元 B、20元 C、25元 D、30元

查看试题解析
2. 甲、乙两人骑车分别从A、B两地同时出发，沿同一路线匀速骑行，两人先相向而行，甲到达B地后停留20min 再以原速返回A地，当两人到达A地后停止骑行.设甲出发x min后距离A地的路程为y km.图中的折线表示甲在整个骑行过程中y与x的函数关系.在整个骑行过程中，两人只相遇了1次，乙的骑行速度（单位：km/min）可能是（）

A、0.1 B、0.15 C、0.2 D、0.25

查看试题解析
3. 一次函数 $y = \frac{1}{2} x - 1$ 的图象与y轴交点是（　　）

A、（﹣1，0） B、（2，0） C、（0，1） D、（0，﹣1）

查看试题解析
4. 无论m为何实数．直线 $y = x + 2 m$ 与 $y = - x + 4$ 的交点不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 已知直线 $l_{1}$ 交x轴于点 $(- 3 ， 0)$ ，交 $y$ 轴于点 $(0 ， 6)$ ，直线 $l_{2}$ 与直线 $l_{1}$ 关于x轴对称，将直线 $l_{1}$ 向下平移8个单位得到直线 $l_{3}$ ，则直线 $l_{2}$ 与直线 $l_{3}$ 的交点坐标为（）

A、 $(- 1 ， - 4)$ B、 $(- 2 ， - 4)$ C、 $(- 2 ， - 1)$ D、 $(- 1 ， - 1)$

查看试题解析
6. 已知一次函数y＝kx+b的图象如图，则不等式ax+b≥2的解集为（）

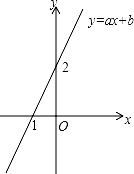A、x＜1 B、x＞1 C、x＝0 D、x≥0

查看试题解析
7. 下列四个选项中，不符合直线 $y = \frac{1}{2} x - 3$ 的性质与特征的是（）

A、经过第一、三、四象限 B、y随x的增大而增大 C、与x轴交于点 $(- 2 ， 0)$ D、与y轴交于点 $(0 ， - 3)$

查看试题解析
8. 某品牌鞋子的长度ycm与鞋子的码数x之间满足一次函数关系．若23码鞋子的长度为16.5cm，44码鞋子的长度为27cm，则38码鞋子的长度为（）

A、23cm B、24cm C、25cm D、26cm

查看试题解析
9. 一次函数y₁＝ax+b与y₂＝cx+d的图象如图所示，下列说法：
①对于函数y＝ax+b来说，y随x的增大而减小；

②函数y＝ax+d的图象不经过第一象限；

③不等式ax+b＞cx+d的解集是x＞3；

④d﹣b＝3（a﹣c）.其中正确的有（）

A、①③ B、②③④ C、①②④ D、②③

查看试题解析
10. 如图，在平面直角坐标系中，点P（-0.5，a）在直线y=2x+2与直线y=2x+4之间，则a的取值范围是（）

A、2＜a＜4 B、1＜a＜3 C、1＜a＜2 D、0＜a＜2

查看试题解析

二、填空题

11. 某长途汽车客运公司规定旅客可免费携带一定质量的行李.当行李的质量超过规定时，需付的行李费y（元）与行李质量 $x (kg)$ 之间满足一次函数关系，部分对应值如下表：

$x (kg)$

…

30

40

50

…

y（元）

…

4

6

8

…

则旅客最多可免费携带行李的质量是kg.

查看试题解析
12. 如图，一次函数 $y = \frac{4}{3}$ x+4的图象与x轴交于点A，与y轴交于点B，C是x轴上的一动点，连接BC，将 $△ A B C$ 沿BC所在的直线折叠，当点A落在y轴上时，点C的坐标为.

查看试题解析
13. 点A（﹣1，y₁），B（3，y₂）是直线y＝kx+b上的两点，若k＜0，则y₁﹣y₂0（填“＞”或“＜”）．

查看试题解析
14. 一次函数y₁＝kx-1（k是常数，且k≠0）和y₂＝x＋1图象的交点始终在第三象限，则k的取值范围是.

查看试题解析
15. 已知直线y=x+b和y=ax+2交于点P（3，-1），则关于x的方程（a-1）x=b-2的解为．

查看试题解析

三、解答题

16. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（km）与甲车行驶的时间t（h）之间的函数关系如图所示．

(1)、A，B两城相距千米；

(2)、当1≤t≤4时，求乙车离开A城的距离y（km）与甲车行驶的时间t（h）之间的函数关系式；

(3)、乙车出发后小时追上甲车．

查看试题解析
17. 如图，直线 $l_{1}$ ， $l_{2}$ 相交于点 $P$ ，直线 $l_{1}$ 的函数表达式为 $y = 3 x + 7$ ，点 $P$ 的横坐标为 $- 2$ ，且直线 $l_{2}$ 与 $y$ 轴交于点 $A (0 ， - 2)$ ，求直线 $l_{2}$ 的函数表达式.

查看试题解析
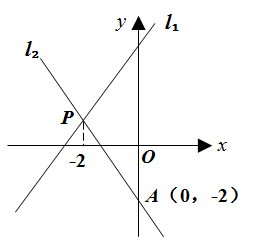18. 用[x]表示不大于x的最大整数，如[2.1]=2，[-4.5]=-5，已知x₁ ，x₂是方程6x+7=3[x]的解，且x₁<x₂ ，点A(x₁ ， y₁)和B (x₂ ， y₂)是直线y=-2x-1上的两点，试比较y₁与y₂+l的大小。

查看试题解析
19. 已知一次函数 $y = k x + b$ 的图象经过点 $(- 2, 5)$ ，并且与 $y$ 轴相交于点 $P$ ，直线 $y = - \frac{1}{2} x + 3$ 与 $y$ 轴相交于点 $Q$ ，点 $Q$ 与点 $P$ 关于 $x$ 轴对称，求这个一次函数的解析式.

查看试题解析
20. 如图，一次函数y $= - \frac{3}{4}$ x+6与坐标轴交于A、B两点，求点A、B的坐标.

查看试题解析
21. 已知直线 $y_{1}$ ＝ $- \frac{2}{3} x + 3$ 与x轴交于点A，与y轴交于点B，直线 $y_{2}$ ＝2x＋b经过点B，且与x轴交于点C，求△ABC的面积.

查看试题解析
22. 大鹏新区某住宅小区计划购买并种植甲、乙两种树苗共300株．已知甲种树苗每株60元，乙种树苗每株90元．设购买甲种树苗x株，购买两种树苗总费用为y元．

(1)、求y与x函数关系式；

(2)、若100≤x≤225时，如何购买甲、乙两种树苗才能保证费用最低？最低费用是多少？

查看试题解析
23. 已知一次函数y=kx﹣4，当x=2时，y=﹣3．

(1)、求一次函数的解析式；

(2)、将该函数的图象向上平移6个单位，求平移后的图象与x轴的交点的坐标．

查看试题解析

$x (kg)$	…	30	40	50	…
y（元）	…	4	6	8	…

（北师大版）2022-2023学年度第一学期八年级数学4.4一次函数的应用 同步测试

一、单选题

二、填空题

三、解答题

（北师大版）2022-2023学年度第一学期八年级数学4.4一次函数的应用同步测试