（北师大版）2022-2023学年度第一学期九年级数学 应用一元二次方程 期中复习
试卷更新日期：2022-10-20 类型：复习试卷
一、单选题
-
1. 如图，在宽为、长为的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要 ， 则修建的路宽应为（ ）
A、 B、 C、 D、2. 某牧民要围成面积为35的矩形羊圈，且长比宽多2米，则此羊圈的周长是（ ）A、20米 B、24 米 C、26 米 D、20或22米3. 某广场有一块正方形的空地正中间修建一个圆形喷泉，在四个角修建四个四分之一圆形的水池，其余部分种植花草，若喷泉和水池的半径都相同，喷泉边缘到空地边界的距离为3m，种植花草的区域的面积为100m，设水池半径为xm，可列出方程（ ）
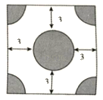A、（2x+3）2﹣πx2＝100 B、（x+6）2﹣πx2＝100 C、（2x+3）2﹣2x2＝100 D、（2x+6）2﹣2πx2＝1004. 李明去参加聚会，每两人都互相赠送礼物，他发现共送礼物30件，若设有n人参加聚会，根据题意可列出方程为（ ）A、 B、n（n﹣1）＝30 C、30 D、n（n＋1）＝305. 如图，在△ABC中，AB＝AC＝6，∠BAC＝120°，过点A作AD⊥BA交BC于点D，过点D作DE⊥BC交AC于点E，则AE的长为（ ）
A、1 B、2 C、3 D、46. 南宋著名数学家杨辉所著的《杨辉算法》中记载：“直田积八百六十四步，只云长阔共六十步，问长阔各几何？”意思是“一块矩形田地的面积是864平方步，只知道它的长与宽的和是60步，问它的长和宽各是多少步？”设矩形田地的长为x步，根据题意可以列方程为（ ）A、 B、 C、 D、7. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送2450张照片，如果全班有x名同学，根据题意，列出方程为（ ）A、x（x+1）＝2450 B、x（x-1）＝2450 C、 x（x+1）＝2450 D、x（x-1）＝24508. 早期，甲肝流行，在一天内，一人能传染4人，若有三人患上甲肝，那么经过两天患上甲肝的人数为（ ）A、50 B、75 C、25 D、709. 《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：“直田积八百六十四步，之云阔不及长一十二步，问阔及长各几步？”译文：“一个矩形田地的面积等于864平方步，且它的宽比长少12步，问长与宽各是多少步？”若设矩形田地的长为x步，则可列方程为（ ）A、2x+2（x+12）＝864 B、2x+2（x﹣12）＝864 C、x（x+12）＝864 D、x（x﹣12）＝86410. 某商场在销售一种日用品时发现，如果以单价20元销售，则每周可售出100件，若销售单价每提高0.5元，则每周销售量会相应减少2件．如果该商场这种日用品每周的销售额达到2024元．若设这种日用品的销售单价为x元，则根据题意所列方程正确的是（ ）A、（20+x）（100﹣2x）＝2024 B、（20+x）（100﹣）＝2024 C、x[100﹣2（x﹣20）]＝2024 D、x（100﹣×2）＝2024二、填空题
-
11. “新冠肺炎”防治取得战略性成果，若有一个人患了“新冠肺炎”，经过两轮传染后共有25个人患了“新冠肺炎”，则每轮传染中平均一个人传染了人．12. 有一个人患了流感，经过两轮传染后共有16个人患了流感，则每轮传染中平均一个人传染个人．13. 某小区中央花园有一块长方形花圃，它的宽为5m，若长边不变，将短边扩大，使得扩大后的花圃形状为正方形，且面积比原来增加15m2 ， 设原来花圃长边为xm，可列方程 ．14. 如图用一段长为16m的篱笆围成一个一边靠墙的矩形围栏（墙长9m），则这个围栏的最大面积为 ．
15. 如图，某小区计划在一块长为 ， 宽为的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为 ， 则道路宽为 ．
三、解答题
-
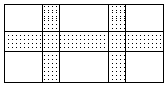
16. 2022年冬季奥运会和冬季残奥会两件赛事在我国首都北京和河北省石家庄市举行，某商家购进了冬季残奥会吉祥物“雪容融”纪念品，每个的进价是30元．为了增大“雪容融”类纪念品的销售量，商家决定对“雪容融”类纪念品进行降价销售，当销售价为每个44元时，每天可以售出20个，每降价1元，每天将多售出5个．请问商家应将“雪容融”类纪念品每个降价多少元时，每天售出此类纪念品能获利400元？17. 某童装店每天卖童装20件，每件盈利40元，为减少库存量，准备在十一期间做活动，若每件童装降价4元，则可多售出8件，此服装店打算在活动期间盈利1200元，则每件童装应降价多少元？18. 如下图所示，在宽为20m，长为32m的矩形耕地上，修筑同样宽的三条道路（互相垂直），把耕地分成大小不等的六块试验田，要使试验田的面积为 ， 道路应为多宽？
19. 如图，点P是边长为6cm的正方形ABCD内部一点，过点P分别作AB，AD的平行线，将正方形分成一、二、三、四共四个不重合的部分，其中第一部分是边长小于3cm的正方形．当第一、四部分的面积和是第二、三部分面积和的3倍时，求第一部分的边长．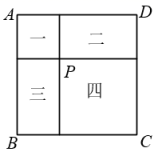
20. 列方程解下列应用题：沈阳的冬天比较冷，某店销售的充电暖宝热销，每个暖宝售价为80元，每星期可卖出300个，为了促销，该店决定降价销售．市场调查反映：每降价1元，每星期可多卖30个．已知该款暖宝每个成本为60元，在顾客得到实惠的前提下，该店还想获得6480元的利润，应将每件的售价定为多少元？21. 某商店进了一批衬衫，平均每天可售出20件，每件盈利40元.为了扩大销售，增加盈利，使库存减少最快，商场决定采取适当的降价措施，经调查发现，如果每件衬衫降价1元，商场平均每天多售出2件，当每件衬衫降价多少元时，商场平均每天盈利达到1200元？22. 某商店将进价为每件10元的商品以每件14元的价格售出，平均每天能售出220件．经市场调查发现：这种商品每件的售价每上涨1元，其销售量就将减少20元，该商店计划通过提高售价减少销售量的办法来增加利润．若物价部门规定此种商品每件利润不能超过进价的80%，且商店想要获得平均每天1080元的利润，则这种商品的售价应定为多少元？23. 在“乡村振兴”行动中，某村办企业开发了一种成本价为50元/盒的有机产品，如果每盒的售价为60元时，每天可以销售200盒，通过市场调查发现，每盒售价每提高1元，每天少卖出10盒．该村办企业要想每天获得2240元利润，该有机产品的售价可以定为多少元/盒？