（北师大版）2022-2023学年度第一学期九年级数学解一元二次方程期中复习

试卷更新日期：2022-10-20 类型：复习试卷

进入出卷网下载

一、单选题

1. 用配方法解方程x²-2x=2时，配方后正确的是（）

A、（x+1）²=3 B、（x+1）²=6 C、（x-1）²=3 D、（x-1）²=6

查看试题解析
2. 用配方法解方程 $x^{2}$ +4x+1＝0时，原方程应变形为（）

A、 ${(x - 2)}^{2} = 3$ B、 ${(x - 2)}^{2} = 5$ C、 ${(x + 2)}^{2} = 5$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
3. 将方程 $x^{2} - 2 x - 3 = 0 化为 {(x - m)}^{2} = n$ 的形式，指出 $m ， n$ 分别是（）

A、1和3 B、-1和3 C、1和4 D、-1和4

查看试题解析
4. 一元二次方程x²+4x﹣11=0配方后化为（　　）

A、（x+4）²=13 B、（x﹣2）²=15 C、（x+2）²=13 D、（x+2）²=15

查看试题解析
5. 一元二次方程x²﹣2x﹣1＝0的根是（）

A、x₁＝1，x₂＝2 B、x₁＝﹣1，x₂＝﹣2 C、x₁＝1+ $\sqrt{2}$ ，x₂＝1﹣ $\sqrt{2}$ D、x₁＝1+ $\sqrt{3}$ ，x₂＝1﹣ $\sqrt{3}$

查看试题解析
6. 对于两个不相等的实数 $a ， b$ ，我们规定符号 $max {a ， b}$ 表示 $a ， b$ 中较大的数，如 $\max {2 ， 4} = 4$ ，按这个规定，方程 $\max {x ， - x} = \frac{2 x + 1}{x}$ 的解为（）

A、 $1 - \sqrt{2}$ B、 $2 - \sqrt{2}$ C、 $1 - \sqrt{2} 或 1 + \sqrt{2}$ D、 $1 + \sqrt{2}$ 或-1

查看试题解析
7. 小丽同学想用公式法解方程 $- x^{2} + 3 x = 1$ ，你认为a，b，c的值分别是（）

A、 $- 1$ 、3、 $- 1$ B、 $- 1$ 、3、1 C、 $- 1$ 、 $- 3$ 、 $- 1$ D、1、 $- 3$ 、 $- 1$

查看试题解析
8. 定义一种新运算：a♣b=a（a﹣b），例如，4♣3=4×（4﹣3）=4，若x♣2=3，则x的值是（）

A、x=3 B、x=﹣1 C、x1=3，x2=1 D、x1=3，x2=﹣1

查看试题解析
9. 方程 $x^{2} + 4 x + 3 = 0$ 的两个根为（）

A、 $x_{1} = 1 ， x_{2} = 3$ B、 $x_{1} = - 1 ， x_{2} = 3$ C、 $x_{1} = 1 ， x_{2} = - 3$ D、 $x_{1} = ﹣ 1 ， x_{2} = ﹣ 3$

查看试题解析
10. 方程 $(x - 2) (x + 3) = 0$ 的解是（）

A、 $x = 2$ B、 $x = 3$ C、 $x_{1} = - 2 ， x_{2} = 3$ D、 $x_{1} = 2 ， x_{2} = - 3$

查看试题解析

二、填空题

11. 将方程x²﹣4x＝2配方成（x+a）²＝b（b≥0）的形式时，则ba＝．

查看试题解析
12. 将一元二次方程 $x^{2} - 6 x - 5 = 0$ 化成 $(x - a)^{2} = b$ 的形式，那么 $a + b$ 的值为．

查看试题解析
13. 已知代数式x²-3与代数式 $- x$ 的值互为相反数，那么x的值为．

查看试题解析
14. 关于x的方程a（x+m）²+b=0的根是x₁=4，x₂=-6，（a，b，m均为常数，a≠0），则关于x的方程a（x+m-3）²+b=0的根是．

查看试题解析
15. 已知一元二次方程 $x^{2} - 14 x + 48 = 0$ 的两个根是菱形的两条对角线长，则这个菱形的周长．

查看试题解析

三、解答题

16. 解方程：
（1）x²+2x﹣9999=0（用配方法求解）；
（2）3x²﹣6x﹣1=0（用公式法求解）

查看试题解析
17. 解方程：
（1）2x²﹣3x﹣1=0
（2） $\frac{1}{x - 2}$ = $\frac{1 - x}{2 - x}$ ﹣3．

查看试题解析
18. 先化简，再求值： $(\frac{x^{2} - 2 x + 4}{x - 1} + 2 - x) \div \frac{x^{2} + 4 x + 4}{1 - x}$ ，其中 $x$ 满足 $x^{2} - 4 x + 3 = 0$ ．

查看试题解析
19. 三角形的两边长分别为3和4，第三边的长是方程x²﹣8x+15=0的解，求此三角形的面积

查看试题解析

四、综合题

20. 有n个方程：x²+2x﹣8=0；x²+2×2x﹣8×2²=0；…x²+2nx﹣8n²=0．
小静同学解第一个方程x²+2x﹣8=0的步骤为：“①x²+2x=8；②x²+2x+1=8+1；③（x+1）²=9；④x+1=±3；⑤x=1±3；⑥x₁=4，x₂=﹣2．”

(1)、小静的解法是从步骤开始出现错误的．

(2)、用配方法解第n个方程x²+2nx﹣8n²=0．（用含有n的式子表示方程的根）

查看试题解析
21. 我们知道，解一元二次方程，可以把它转化为两个一元一次方程来解，其实用“转化”的数学思想我们还可以解一些新的方程例如一元三次方程x³+x²﹣2x＝0，可以通过因式分解把它转化为x（x²+x﹣2）＝0，通过解方程x＝0和x²+x﹣2＝0，可得方程x³+x²﹣2x＝0的解．

(1)、方程x³+x²﹣2x＝0的解是x₁＝0，x₂＝， x₃＝．

(2)、用“转化”的思想求方程 $\sqrt{2 x + 3}$ ＝x的解．

(3)、试直接写出 ${\begin{array}{l} x^{2} - 4 y^{2} = 0 \\ x + y = 1 \end{array}$ 的解．

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，以点B为圆心，BC长为半径画弧，交边AB与点D，连接CD．

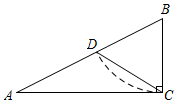(1)、若∠A＝28°，求∠ACD的度数；

(2)、若BC＝1，AC＝a．
①直接写出线段AD的长为（用含字母a的式子表示）；

②判断线段AD的长是方程x²+2x﹣a²＝0的一个根吗？为什么？

查看试题解析
23. 如果关于x的一元二次方程 $a x^{2} + b x + c = 0$ （ $a \neq 0$ ， a，b，c是常数）有两个实数根，且其中一个根为另一个根的一半时，那么称这样的方程为“半根方程”．例如，一元二次方程 $(x - 3) (x - 6) = 0$ 的两个根是3和6，该方程可化简为 $x^{2} - 9 x + 18 = 0$ ，则方程 $x^{2} - 9 x + 18 = 0$ 就是半根方程．

(1)、请你再写出一个半根方程（要求化成一般形式）；

(2)、若关于x的方程 $(2 x - 1) (m x - n) = 0 (m \neq 0)$ 是半根方程，求 $\frac{n}{m - n}$ 的值．

查看试题解析

（北师大版）2022-2023学年度第一学期九年级数学解一元二次方程 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

（北师大版）2022-2023学年度第一学期九年级数学解一元二次方程期中复习