(北师大版)2022-2023学年度第一学期九年级数学正方形的性质与判定 期中复习
试卷更新日期:2022-10-20 类型:复习试卷
一、单选题
-
1. 如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形 , 依此方式连续旋转2023次得到正方形 , 那么点的坐标是( )
 A、(a,a) B、 C、 D、2. 如图,以菱形的边为对角线,作正方形 , 点恰好落在的延长线上,则的度数是( )
A、(a,a) B、 C、 D、2. 如图,以菱形的边为对角线,作正方形 , 点恰好落在的延长线上,则的度数是( ) A、 B、 C、 D、3. 如图,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
A、 B、 C、 D、3. 如图,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( ) A、AC=BC=CD=DA B、AO=BO=CO=DO,AC⊥BD C、AO=CO,BO=DO,AC⊥BD D、AB=BC,CD⊥DA4. 如图,以的两直角边为边向外作正方形,其面积分别为 , , 若 , , 则斜边的长是( )
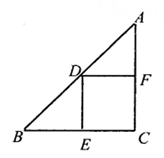
A、AC=BC=CD=DA B、AO=BO=CO=DO,AC⊥BD C、AO=CO,BO=DO,AC⊥BD D、AB=BC,CD⊥DA4. 如图,以的两直角边为边向外作正方形,其面积分别为 , , 若 , , 则斜边的长是( )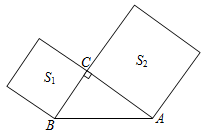 A、3 B、4 C、5 D、255. 如图,在中,点、、分别在边 , , 上,且 , 下列结论:①四边形是平行四边形;②如果 , 那么四边形是矩形;③如果平分 , 那么四边形是菱形;④如果 , 平分 , 那么四边形是正方形你认为正确的是( )
A、3 B、4 C、5 D、255. 如图,在中,点、、分别在边 , , 上,且 , 下列结论:①四边形是平行四边形;②如果 , 那么四边形是矩形;③如果平分 , 那么四边形是菱形;④如果 , 平分 , 那么四边形是正方形你认为正确的是( ) A、①②③④ B、①②③ C、①②④ D、②③④6. 正方形具有而矩形不一定有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角互补 D、四个角相等7. 如图,正方形ABCD中,点E是对角线AC上的一点,且连接DE,则∠CDE的度数为( )
A、①②③④ B、①②③ C、①②④ D、②③④6. 正方形具有而矩形不一定有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角互补 D、四个角相等7. 如图,正方形ABCD中,点E是对角线AC上的一点,且连接DE,则∠CDE的度数为( ) A、20° B、22.5° C、25° D、30°8. 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3 , 则点A3到x轴的距离是( ).
A、20° B、22.5° C、25° D、30°8. 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3 , 则点A3到x轴的距离是( ). A、 B、 C、 D、9. 如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A、 B、 C、 D、9. 如图,四边形ABCD是平行四边形,下列结论中错误的是( ) A、当▱ABCD是矩形时,∠ABC=90° B、当▱ABCD是菱形时,AC⊥BD C、当▱ABCD是正方形时,AC=BD D、当▱ABCD是菱形时,AB=AC10. 下列条件中,能判定四边形是正方形的是( )A、对角线相等的平行四边形 B、对角线互相平分且垂直的四边形 C、对角线互相垂直且相等的四边形 D、对角线相等且互相垂直的平行四边形
A、当▱ABCD是矩形时,∠ABC=90° B、当▱ABCD是菱形时,AC⊥BD C、当▱ABCD是正方形时,AC=BD D、当▱ABCD是菱形时,AB=AC10. 下列条件中,能判定四边形是正方形的是( )A、对角线相等的平行四边形 B、对角线互相平分且垂直的四边形 C、对角线互相垂直且相等的四边形 D、对角线相等且互相垂直的平行四边形二、填空题
-
11. 如图,在正方形ABCD中,AB=4 . E、F分别为边AB、BC的中点,连接AF、DE,点N、M分别为AF、DE的中点,连接MN,则MN的长度为 .
 12. 如图,正方形ABCD的边长为4,E是BC的中点,在对角线BD上有一点P,则PC+PE的最小值是.
12. 如图,正方形ABCD的边长为4,E是BC的中点,在对角线BD上有一点P,则PC+PE的最小值是.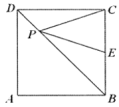 13. 如图,在边长为2的正方形ABCD 中,E,F分别是边DC,CB上的动点,且始终满足DE=CF,AE,DF交于点 P,则∠APD的度数为 ;连接CP,线段CP长的最小值为 .
13. 如图,在边长为2的正方形ABCD 中,E,F分别是边DC,CB上的动点,且始终满足DE=CF,AE,DF交于点 P,则∠APD的度数为 ;连接CP,线段CP长的最小值为 . 14. 如图,在正方形ABCD中,AB=2,取AD的中点E,连接EB,延长DA至F,使EF=EB,以线段AF为边作正方形AFGH,点H在线段AB上,则的值是 .
14. 如图,在正方形ABCD中,AB=2,取AD的中点E,连接EB,延长DA至F,使EF=EB,以线段AF为边作正方形AFGH,点H在线段AB上,则的值是 . 15. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
15. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
三、解答题
-
16. 如图,E是正方形ABCD对角线BD上的一点,求证:AE=CE.
 17. 已知:如图,在 中, , 是 的角平分线, , ,垂足分別为E、F.求证:四边形 是正方形.
17. 已知:如图,在 中, , 是 的角平分线, , ,垂足分別为E、F.求证:四边形 是正方形. 18. 如图,在正方形ABCD中,点E,F分别是BC,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.观察:EF,DF,BE三条线段都不在同一条直线上,能不能借助图形的运动,将部分线段放置在一条直线上加以证明呢?思路:将△ABE绕点A顺时针旋转9O°使AB与AD重合,得到了旋转后的△ADG.
18. 如图,在正方形ABCD中,点E,F分别是BC,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.观察:EF,DF,BE三条线段都不在同一条直线上,能不能借助图形的运动,将部分线段放置在一条直线上加以证明呢?思路:将△ABE绕点A顺时针旋转9O°使AB与AD重合,得到了旋转后的△ADG.
①根据上述思路在图中画图分析并证明(写出详细的证明过程).
②若正方形ABCD的边长为6,当动点E在BC边上运动到中点位置时,动点F在CD边上距离D点多长的位置?
19. 如图,在正方形 中,点E、F分别在 上,且 是等边三角形.
求证: .
20. 已知,如图,在Rt△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF,当点D在线段BC的反向延长线上,且点A,F分别在直线BC的两侧时. (1)、求证:△ABD≌△ACF;(2)、若正方形ADEF的边长为 ,对角线AE,DF相交于点O,连接OC,求OC的长度.
(1)、求证:△ABD≌△ACF;(2)、若正方形ADEF的边长为 ,对角线AE,DF相交于点O,连接OC,求OC的长度.