(北师大版)2022-2023学年度第一学期九年级数学矩形的性质与判定 期中复习
试卷更新日期:2022-10-20 类型:复习试卷
一、单选题
-
1. 如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:

① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A、① B、①② C、①③ D、①②③2. 如图,在矩形ABCD中,AD=10,AB=6,E为BC上一点,DE平分∠AEC,则CE的长为( )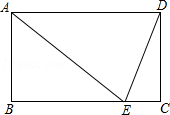 A、1 B、2 C、3 D、43. 矩形与矩形如图放置,点、、共线,点、、共线,连接 , 取的中点 , 连接若 , , 则( )
A、1 B、2 C、3 D、43. 矩形与矩形如图放置,点、、共线,点、、共线,连接 , 取的中点 , 连接若 , , 则( )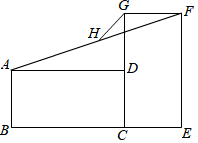 A、 B、 C、 D、4. 如图是一张矩形纸片 , 点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接 , 若 , 则 度
A、 B、 C、 D、4. 如图是一张矩形纸片 , 点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接 , 若 , 则 度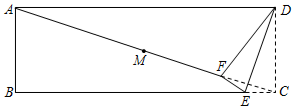 5. AC,BD是▱的两条对角线,如果添加一个条件,使▱为矩形,那么这个条件可以是( )A、 B、 C、 D、6. 在平行四边形ABCD中,AB=3,BC=4,当平行四边形ABCD的面积最大时,①BD=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.以上4个结论中正确的有( )A、①②③ B、①②④ C、②③④ D、①③④7. 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )
5. AC,BD是▱的两条对角线,如果添加一个条件,使▱为矩形,那么这个条件可以是( )A、 B、 C、 D、6. 在平行四边形ABCD中,AB=3,BC=4,当平行四边形ABCD的面积最大时,①BD=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.以上4个结论中正确的有( )A、①②③ B、①②④ C、②③④ D、①③④7. 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )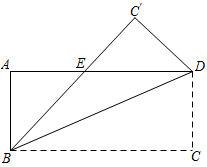 A、3 B、4 C、5 D、68. 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在边AB上的点C′上,且GE=GC′,若DE=3,AB=6,BC=9,则BF的长为( )
A、3 B、4 C、5 D、68. 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在边AB上的点C′上,且GE=GC′,若DE=3,AB=6,BC=9,则BF的长为( ) A、4 B、3 C、4.5 D、59. 如图,将矩形ABCD放置在平面直角坐标系的第一象限内,使顶点A,B分别在x轴、y轴上滑动,矩形的形状保持不变,若AB=2,BC=1,则顶点C到坐标原点O的最大距离为( )
A、4 B、3 C、4.5 D、59. 如图,将矩形ABCD放置在平面直角坐标系的第一象限内,使顶点A,B分别在x轴、y轴上滑动,矩形的形状保持不变,若AB=2,BC=1,则顶点C到坐标原点O的最大距离为( ) A、1+ B、1+ C、3 D、10. 如图,扇形AOB的圆心角为90°,四边形OCDE是边长为1的正方形,点C,E,D分别在OA,OB, 上,过A作AF⊥ED交ED的延长线于点F,那么图中阴影部分的面积为( )
A、1+ B、1+ C、3 D、10. 如图,扇形AOB的圆心角为90°,四边形OCDE是边长为1的正方形,点C,E,D分别在OA,OB, 上,过A作AF⊥ED交ED的延长线于点F,那么图中阴影部分的面积为( ) A、 B、 ﹣1 C、2﹣ D、
A、 B、 ﹣1 C、2﹣ D、二、填空题
-
11. 如图,在矩形ABCD中,E,F分别是AD,AB的中点,若AC=4,则EF的长是.
 12. 如图,在矩形中, , 对角线的长为5,作的垂直平分线交于点 , 连接 , 则的周长为 .
12. 如图,在矩形中, , 对角线的长为5,作的垂直平分线交于点 , 连接 , 则的周长为 . 13. 如图,将一矩形纸片折叠,使两个顶点 , 重合,折痕为若 , , 则的长为 .
13. 如图,将一矩形纸片折叠,使两个顶点 , 重合,折痕为若 , , 则的长为 . 14. 如图,在菱形ABCD中,E,F,G分别是AD,AB,CD的中点,且 , , 则菱形ABCD的面积是 .
14. 如图,在菱形ABCD中,E,F,G分别是AD,AB,CD的中点,且 , , 则菱形ABCD的面积是 . 15. 如图,矩形中,于点 , 若 , 则度.
15. 如图,矩形中,于点 , 若 , 则度.
三、解答题
-
16. 如图,点A在∠MON的边ON上,AB⊥OM于点B,AE=OB,DE⊥ON于点E,AD=AO,DC⊥OM于点C,求证:四边形ABCD是矩形.
 17. 如图,△ABC中,点D是边AC的中点,过D作直线PQ∥BC,∠BCA的平分线交直线PQ于点E,点G是△ABC的边BC延长线上的点,∠ACG的平分线交直线PQ于点F.求证:四边形AECF是矩形.
17. 如图,△ABC中,点D是边AC的中点,过D作直线PQ∥BC,∠BCA的平分线交直线PQ于点E,点G是△ABC的边BC延长线上的点,∠ACG的平分线交直线PQ于点F.求证:四边形AECF是矩形.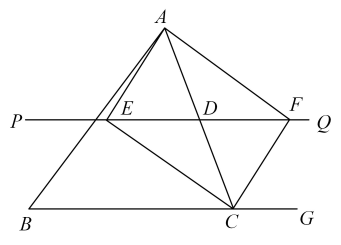 18. 如图,在中,对角线AC与BD交于点O,于点H,且 , 求证:是矩形.
18. 如图,在中,对角线AC与BD交于点O,于点H,且 , 求证:是矩形. 19. 如图,在矩形ABCD中,AC交BD于点E,且四边形AEBF为菱形,已知BD=2BC=8,求FD与四边形ADEF的面积.
19. 如图,在矩形ABCD中,AC交BD于点E,且四边形AEBF为菱形,已知BD=2BC=8,求FD与四边形ADEF的面积.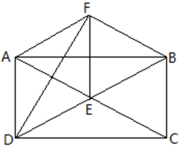 20. 在Rt△ABC中,∠C=90°,D,E,F分别是AC,AB,BC的中点,连接ED,EF.求证:四边形DEFC是矩形.
20. 在Rt△ABC中,∠C=90°,D,E,F分别是AC,AB,BC的中点,连接ED,EF.求证:四边形DEFC是矩形.


