（北师大版）2022-2023学年度第一学期九年级数学菱形的性质与判定期中复习

试卷更新日期：2022-10-20 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，在菱形ABCD中，对角线AC、BD交于点O，已知AO＝2，OB＝4，则菱形ABCD的面积是（）

A、4 B、8 C、16 D、20

查看试题解析
2. 如图，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于H，连接OH，∠DHO＝α，则∠DAB的度数是（）

A、α B、2α C、90°﹣α D、90°﹣2α

查看试题解析
3. 如图，在菱形 $A B C D$ 中， $∠ B = 60 °$ ， $B C = 6$ ， $E$ 为 $B C$ 中点， $F$ 是 $A B$ 上一点， $G$ 为 $A D$ 上一点，且 $B F = 2$ ， $∠ F E G = 60 °$ ， $E G$ 交 $A C$ 于点 $H$ ，关于下列结论，正确序号的选项是（）
① $Δ B E F ∽ Δ C H E$ ， ② $A G = 1$ ， ③ $E H = \frac{3}{2} \sqrt{7}$ ④ $S_{Δ B E F} = 3 S_{Δ A G H}$

A、①② B、①②③ C、①②④ D、①③④

查看试题解析
4. 如图，在菱形 $ABCD$ 中， $AC$ 与 $BD$ 相交于点 $O$ ， $AB$ 的垂直平分线 $EF$ 交 $AC$ 于点 $F$ ，连接 $DF$ ，若 $∠ BAD = 80 °$ ，则 $∠ CDF$ 的度数为（）

A、 $60 °$ B、 $80 °$ C、 $85 °$ D、 $100 °$

查看试题解析
5. 如图，在矩形 $A B C D$ 中， $A B = 24$ ， $B C = 12$ ，点 $E$ 在边 $A B$ 上，点 $F$ 在边 $C D$ 上，点 $G$ 、 $H$ 在对角线 $A C$ 上，若四边形 $E G F H$ 是菱形．则 $A E$ 的长是（）

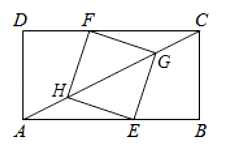A、15 B、20 C、 $6 \sqrt{3}$ D、 $8 \sqrt{3}$

查看试题解析
6. 菱形、矩形同时具有的性质是（）

A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补

查看试题解析
7. 如图，在菱形ABCD中， $A B = 4$ ， $∠ B A D = 120 °$ ， $△ A E F$ 为等边三角形点E，F分别在菱形的边BC，CD上滑动，且E，F不与B，C，D重合，则四边形AECF的面积是（）

A、4 B、 $4 \sqrt{3}$ C、8 D、 $8 \sqrt{3}$

查看试题解析
8. 如图，菱形 $A B C D$ 的对角线 $B D = 12$ ， $A C = 10$ ，则该菱形的面积为（）．

A、60 B、80 C、100 D、120

查看试题解析
9. 如图，在菱形ABCD中，∠A＝60°，AB＝8cm，则菱形ABCD的面积是（　　）cm²

A、16 $\sqrt{3}$ B、32 $\sqrt{3}$ C、64 $\sqrt{3}$ D、32 $\sqrt{2}$

查看试题解析
10. 如图，已知菱形ABCD的周长为24，对角线AC、BD交于点O，且AC+BD＝16，则该菱形的面积等于（）

A、6 B、8 C、14 D、28

查看试题解析

二、填空题

11. 如图，菱形ABCD中， $A C = 6$ ， $B D = 8$ ， AH为菱形的高，则AH＝．

查看试题解析
12. 如图，在菱形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点 $O$ 、 $H$ 为边 $A D$ 的中点，菱形的周长为48，则 $O H$ 的长是．

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A D = 2 A B$ ，点 $M$ 、 $N$ 分别在边 $A D$ 、 $B C$ 上，连接 $B M$ 、 $D N .$ 若四边形 $M B N D$ 是菱形，则 $\frac{A M}{M D}$ 等于．

查看试题解析
14. 如图，在边长为6的菱形ABCD中，∠DAB=60°，E是AB的中点，F是AC上一个动点，则EF+BF的最小值是 .

查看试题解析
15. 如图，菱形 $A B C D$ 的对角线 $A C ， B D$ 相交于点O，点E是边 $A B$ 的中点，若 $O E = 5.5$ ，则菱形 $A B C D$ 的周长为．

查看试题解析

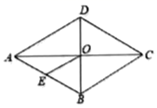
三、解答题

16. 如图，在菱形ABCD中，M，N分别是AB和BC上的点，且AM＝CN，求证：∠DMN＝∠DNM．

查看试题解析
17. 已知：在菱形 $A B C D$ 中，点E，O，F分别为AB，AC，AD的中点，连接 $C E$ ， $C F ， O E ， O F$ .求证： $△ B C E ≌ △ D C F$ ；

查看试题解析
18. 如图，在 $▱ A B C D$ 中，点 $E$ ， $F$ 分别在线段 $B C$ ， $A D$ 上，连接 $A E$ ， $C F$ ， $A E ∥ C F$ ， $B E + A E = A D$ ，求证：四边形 $A E C F$ 是菱形．

查看试题解析
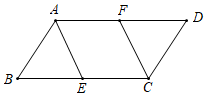19. 如图，已知四边形ABCD是平行四边形，点E，F分别是BC，CD上的点，∠AEB＝∠AFD，BE＝DF．求证：四边形ABCD是菱形．

查看试题解析
20. 如图，点E，F分别在菱形ABCD的边DC，DA上，且CE=AF．求证：∠ABF=∠CBE．

查看试题解析
21. 如图，在等腰△ABC中，AB=AC，AH⊥BC，点E是AH上一点，延长AH至点F，使FH=EH，

求证：四边形EBFC是菱形.

查看试题解析
22. 如图，在△ABC中AC＝BC，D，E，F分别是AB，AC，BC的中点，连接DE，DF.求证：四边形DFCE是菱形.

查看试题解析
23. 如图，在 $△ A B C$ 中， $A C = B C ， D ， E ， F$ 分别是 $A B ， A C ， B C$ 的中点，连接 $D E ， D F$ .求证：四边形 $D F C E$ 是菱形.

查看试题解析

（北师大版）2022-2023学年度第一学期九年级数学菱形的性质与判定 期中复习

一、单选题

二、填空题

三、解答题

（北师大版）2022-2023学年度第一学期九年级数学菱形的性质与判定期中复习