(北师大版)2022-2023学年度第一学期八年级数学 一次函数的应用 期中复习
试卷更新日期:2022-10-20 类型:复习试卷
一、单选题
-
1. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、
 B、
B、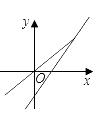 C、
C、 D、
D、 2. 在探究“水沸腾时温度变化特点”的实验中,下表记录了实验中温度和时间变化的数据.
2. 在探究“水沸腾时温度变化特点”的实验中,下表记录了实验中温度和时间变化的数据.时间/分钟
0
5
10
15
20
25
温度/℃
10
25
40
55
70
85
若温度的变化是均匀的,则18分钟时的温度是( )
A、62℃ B、64℃ C、66℃ D、68℃3. 如图,一次函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4,则下列说法正确的个数是( )
①对于函数y=ax+b来说,y随x的增大而减小;②函数y=ax+d不经过第一象限;③方程ax+b=cx+d的解是x=4;④ d-b=4(a-c).
A、1 B、2 C、3 D、44. 巴中某快递公司每天上午7:00﹣8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的个数为( )①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件数量为8件;
③8:00时,甲仓库内快件数为400件;
④7:20时,两仓库快递件数相同.
 A、1个 B、2个 C、3个 D、4个5. 已知点A(3,y1)和点B(﹣2,y2)是一次函数y=﹣2x+3图象上的两点,比较y1与y2的大小关系( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定6. 关于函数y=-2x+1,下列结论正确的是( )A、图象经过点 B、y随x的增大而增大 C、图象不经过第四象限 D、图象与直线y=-2x平行7. 如图所示,一次函数 的图象经过点 ,则方程 的解是( )
A、1个 B、2个 C、3个 D、4个5. 已知点A(3,y1)和点B(﹣2,y2)是一次函数y=﹣2x+3图象上的两点,比较y1与y2的大小关系( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定6. 关于函数y=-2x+1,下列结论正确的是( )A、图象经过点 B、y随x的增大而增大 C、图象不经过第四象限 D、图象与直线y=-2x平行7. 如图所示,一次函数 的图象经过点 ,则方程 的解是( ) A、 B、 C、 D、无法确定8. 在同一平面直角坐标系中,函数 的图象与函数 的图象互相平行,则下列各点在函数 的图象上的点是( )A、 B、 C、 D、9. 已知点 , 在一次函数 的图象上,则 , 的大小关系是( )A、 B、 C、 D、以上都不对10. 如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏;公交公司认为:运营成本难以下降,提高票价才能扭亏;根据这两种意见,把图①分别改画成图②和图③,则下列判断不合理的是( )
A、 B、 C、 D、无法确定8. 在同一平面直角坐标系中,函数 的图象与函数 的图象互相平行,则下列各点在函数 的图象上的点是( )A、 B、 C、 D、9. 已知点 , 在一次函数 的图象上,则 , 的大小关系是( )A、 B、 C、 D、以上都不对10. 如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏;公交公司认为:运营成本难以下降,提高票价才能扭亏;根据这两种意见,把图①分别改画成图②和图③,则下列判断不合理的是( ) A、图①中点A的实际意义是公交公司运营前期投入成本为1万元 B、图②能反映公交公司意见 C、图③能反映乘客意见 D、图②中当乘客量为1.5万时公交公司收支平衡
A、图①中点A的实际意义是公交公司运营前期投入成本为1万元 B、图②能反映公交公司意见 C、图③能反映乘客意见 D、图②中当乘客量为1.5万时公交公司收支平衡二、填空题
-
11. 已知 , 是一次函数的图象上的两个点,则 , 的大小关系是 .12. 已知关于的方程的解为 , 则一次函数与轴交点的坐标为 .13. 已知点( +1,y1),(4,y2)在一次函数y=﹣2x+4图象上,则y1y2(填“>”、“<”或“=”).14. 如图所示为两个一次函数的图象,则关于x,y的方程 的解为 .
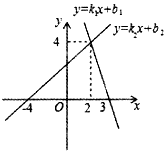 15. 如图,直线l1:y=x+1与x轴交于点A,与直线l2:y= x+2交于点B,点C为x轴上的一点,若△ABC为直角三角形,则点C的横坐标为 .
15. 如图,直线l1:y=x+1与x轴交于点A,与直线l2:y= x+2交于点B,点C为x轴上的一点,若△ABC为直角三角形,则点C的横坐标为 .
三、解答题
-
16. 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围.
 17. 已知: , 与 成正比例, 与x成反比例.当 时, ;当 时, .求y与x的函数解析式.18. 甲,乙两地相距300千米.一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,线段CD对应的函数解析式是y=110x﹣195(2.5≤x≤4.5),在轿车行进过程中,轿车行驶多少时间,两车相距15千米?
17. 已知: , 与 成正比例, 与x成反比例.当 时, ;当 时, .求y与x的函数解析式.18. 甲,乙两地相距300千米.一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,线段CD对应的函数解析式是y=110x﹣195(2.5≤x≤4.5),在轿车行进过程中,轿车行驶多少时间,两车相距15千米?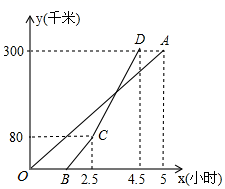 19. 设一次函数y=kx+b的图象过点A(2,﹣1)和点B,其中点B是直线y= x+3与y轴的交点,求这个一次函数的解析式.20. 医药研究所试验某种新药效时,成人如果按剂量服用,血液中每毫升含药量y(毫克)随时间x的变化如图所示,如果每毫升血液中含药量超过4微克(含4微克)时治疗疾病为有效,那么有效时间是多少小时?
19. 设一次函数y=kx+b的图象过点A(2,﹣1)和点B,其中点B是直线y= x+3与y轴的交点,求这个一次函数的解析式.20. 医药研究所试验某种新药效时,成人如果按剂量服用,血液中每毫升含药量y(毫克)随时间x的变化如图所示,如果每毫升血液中含药量超过4微克(含4微克)时治疗疾病为有效,那么有效时间是多少小时? 21. 学完第五章《平面直角坐标系》和第六章《一次函数》后,老师布置了这样一道思考题:已知:如图,在长方形ABCD中,BC=8,AB=4,点E为AD的中点,BD和CE相交于点P.求△BPC的面积. 小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:
21. 学完第五章《平面直角坐标系》和第六章《一次函数》后,老师布置了这样一道思考题:已知:如图,在长方形ABCD中,BC=8,AB=4,点E为AD的中点,BD和CE相交于点P.求△BPC的面积. 小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:
请你按照小明的思路解决这道思考题.
