（北师大版）2022-2023学年度第一学期八年级数学 轴对称与坐标变化 期中复习
试卷更新日期：2022-10-20 类型：复习试卷
一、单选题
-
1. 下列四个命题中，正确的个数有（ ）
①数轴上的点和有理数是一一对应的；②估计的值在 4 和 5 之间；③Rt△ABC 中，已知两边长分别是 3 和 4，则第三条边长为 5；④在平面直角坐标系中点(2，-3)关于x 轴对称的点的坐标是(2，3)；⑤16 的平方根是±4 ，用式子表示是= ±4 ；⑥立方根等于它本身的数有2个．
A、1个 B、2个 C、3个 D、4个2. 已知点M(2，﹣3)，点N与点M关于x轴对称，则点N的坐标是（ ）A、(﹣2，3) B、(﹣2，﹣3) C、(3，2) D、(2，3)3. 在平面直角坐标系中，点的坐标为 ， 则点关于轴对称点的坐标是（ ）A、 B、 C、 D、4. 点P（ 5，－3 ）关于y轴的对称点是 （ ）A、（－5， 3 ） B、（－5，－3） C、（5，3 ） D、（5，－3 ）5. 已知点A 关于 轴的对称点A’与点B 关于 轴的对称点B’重合，则 （ ）A、5 B、1 C、-1 D、-56. 已知点A（m ， 2021）与点B（2020，n）关于x轴对称，则m+n的值为（ ）A、1 B、﹣1 C、0 D、27. 在平面直角坐标系中，点A（2，m）和点B（n ， 3）关于 轴对称，则 的值为（ ）A、5 B、﹣5 C、1 D、﹣18. 已知：点 与点 关于 轴对称，则 的值为（ ）A、0 B、1 C、-1 D、9. 如图是小刚画的一张脸，若用点A(1，1)表示左眼的位置，点B(3，1)表示右眼的位置，则嘴巴点C的位置可表示为（ ）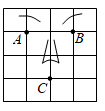
A、(2，﹣1) B、(2，1) C、(3，﹣1) D、(2，0)10. 已知点A(m，2)和点B(－1，n)关于y轴对称，则m＋n的值是（ ）A、1 B、－3 C、3 D、－1二、填空题
-
11. 已知点P（3，1）关于y轴的对称点Q的坐标为 ．12. 在平面直角坐标系中，对进行循环往复的轴对称变换，若原来点的坐标是 ， 则经过第2021次变换后所得的点的坐标是 ．
13. 在平面直角坐标系中，点A（m，﹣4）与点B（﹣5，n）关于y轴对称，则点（m，n）在第 象限．14. 若点（－1，m）与点（n，2）关于y轴对称，则的值为 ．15. 点A关于y轴的对称点 坐标是 ，则点A关于x轴的对称点 坐标是.三、解答题
-
16. 已知点A（a-1，5）和点B（2，b-1）关于x轴对称，求（a+b）2017的值．17. 如图，在平面直角坐标系中有一个△ABC，顶点A（-1，3），B（2，0），C（-3，-1）．
(1)、画出△ABC关于y轴的对称图形△A1B1C1（不写画法）；点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
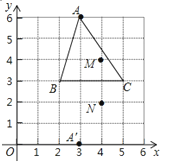
(2)、若网格上的每个小正方形的边长为1，则△ABC的面积是 ．18. 在直角坐标系中，已知A（1，5），B（﹣4，﹣2），C（1，0）三点．(1)、点A关于x轴的对称的A′的坐标为；点B关于y轴的对称点B′的坐标为；点C关于y轴的对称点C′的坐标为 ．(2)、求（1）中的△A′B′C′的面积．19.如图所示，△ABC和△A′BC存在着某种对应关系（它们关于BC对称），其中A的对应点是A′，A（3，6），A′（3，0），△ABC内部的点M（4，4）的对应点是N（4，2）．
（1）你知道它们的对应点的坐标有什么关系吗？
（2）如果△ABC内有一点P（x，y），那么在△A′BC内P的对应点P′的坐标是什么？
20. 已知点A（2a﹣b，5+a），B（2b﹣1，﹣a+b）．（1）若点A、B关于x轴对称，求a、b的值；
（2）若A、B关于y轴对称，求﹙4a+b﹚2014的值．
21.如图，在平面直角坐标系中，函数y=x的图象l是第一、三象限的角平分线．
实验与探究：
由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（﹣2，5）关于直线l的对称点B′、C′的位置，并写出它们的坐标：B′ 、C′ ；
归纳与发现：
结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P（m，n）关于第一、三象限的角平分线L的对称点P′的坐标为 ．
