（北师大版）2022-2023学年度第一学期七年级数学探索与表达规律期中复习

试卷更新日期：2022-10-19 类型：复习试卷

进入出卷网下载

一、单选题

1. 观察下列三行数：
第一行：2、4、6、8、10、12……
第二行：3、5、7、9、11、13……
第三行：1、4、9、16、25、36……
设x、y、z分别为第一、第二、第三行的第100个数，则 $2 x - y + 2 z$ 的值为（）

A、9999 B、10001 C、20199 D、20001

查看试题解析
2. 用木棒按如图所示的规律摆放图形，第100个图形需要木棒根数是（）

A、501 B、502 C、503 D、504

查看试题解析
3. 如图是用黑白两种颜色的正六边形地面砖铺成的图案，依此规律，第n个图案中有（）个白色地面砖（用含有n的代数式表示）.

A、n B、4n－2 C、4n+2 D、4n+6

查看试题解析
4. 已知一列数a₁、a₂、a₃ ， …，满足 $a_{m} \cdot a_{n} = a_{m + n}$ (m，n为正整数)、例如： $a_{1} \cdot a_{2} = a_{1 + 2} = a_{3} ， a_{2} \cdot a_{2} = a_{2 + 2} = a_{4}$ ，若 $a_{1} < 0 ， a_{2} = 4$ ，则 $a_{2021}$ 的值是（ )

A、4042 B、 $- 2^{2020}$ C、 $2^{2021}$ D、 $- 2^{2021}$

查看试题解析
5. 如果a是大于1的正整数，那么a的三次方可以改写成若干个连续奇数的和．例如2³＝3+5，3³＝7+9+11，4³＝13+15+17+19，…，已知a³改写成的若干个连续奇数和的式子中，有一个奇数是2021，则a的值是（）

A、45 B、46 C、52 D、53

查看试题解析
6. 如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加1的规律拼成下列图案，若第 $n$ 个图案中有2023个白色纸片，则 $n$ 的值为（）

A、672 B、673 C、674 D、675

查看试题解析
7. 古希腊数学家把1，3，6，10，15，21，…叫做三角形数，其中1是第一个三角形数，3是第2个三角形数，6是第3个三角形数，…依此类推，那么第7个三角形数（）

A、25 B、27 C、28 D、33

查看试题解析
8. 如图，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三角形中y与n之间的关系是（）

A、y=2ⁿ+1 B、y=2ⁿ+n C、y=2ⁿ⁺¹+n D、y=2ⁿ+n+1

查看试题解析
9. 如图所示的运算程序中，若开始输入的x值为24，我们发现第1次输出的结果为12，第2次输出的结果为6，…，则第2021次输出的结果为（）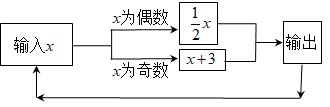

A、6 B、3 C、24 D、12

查看试题解析
10. 观察下列关于 $a$ 的单项式，探究其规律： $a ， 3 a^{2} ， 5 a^{3} ， 7 a^{4} ， 9 a^{5} ， ⋯$ ，按照上述规律，第2022个单项式是（）

A、 $2022 a^{2022}$ B、 $4045 a^{2022}$ C、 $4044 a^{2022}$ D、 $4043 a^{2022}$

查看试题解析

二、填空题

11. 观察下列各式：
1³＝1²
1³+2³＝3²
1³+2³+3³＝6²
1³+2³+3³+4³＝10²
…
猜想1³+2³+3³+…+8³＝．

查看试题解析
12. 如图是一组有规律的图案，第1个图案有4个三角形，第2个图案有7个三角形……按此规律下去，第k个图案有个三角形．（结果用含k的代数式表示）

查看试题解析
13. 一只兔子落在数轴的某点P₀上，第1次从P₀向左跳1个单位到P₁ ，第2次从P₁向右跳2个单位到P₂ ，第3次从P₂向左跳3个单位到P₃ ，第4次从P₃向右跳4个单位到P₄ ， …，若按以上规律跳了100次时，兔子落在数轴上的点P₁₀₀所表示的数恰好是2021，则这只兔子的初始位置P₀所表示的数是．

查看试题解析
14. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第一次点A向左移动3个单位长度到达点 $A_{1}$ ，第2次从点 $A_{1}$ 向右移动6个单位长度到达点 $A_{2}$ ，第3次从点 $A_{2}$ 向左移动9个单位长度到达点 $A_{3}$ ， …，按照这种移动规律进行下去，第n次移动到达点 $A_{n}$ ，如果点 $A_{n}$ 与原点的距离不小于17，那么n的最小值是．

查看试题解析
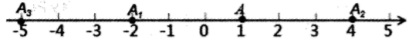15. 观察一列有规律的单项式：x，3x² ， 5x³ ， 7x⁴ ， 9x⁵…，它的第n个单项式是．

查看试题解析

三、解答题

16. 阅读下题的计算方法：
计算 $- 5 \frac{5}{6} + (- 9 \frac{2}{3}) + 17 \frac{3}{4} + (- 3 \frac{1}{2})$ .

解：原式 $= [(- 5) + (- \frac{5}{6})] + [(- 9) + (- \frac{2}{3})] + (17 + \frac{3}{4}) + [(- 3) + (- \frac{1}{2})]$

$= [(- 5) + (- 9) + 17 + (- 3)] + [(- \frac{5}{6}) + (- \frac{2}{3}) + \frac{3}{4} + (- \frac{1}{2})]$

$= 0 + (- \frac{5}{4})$

$= - \frac{5}{4}$

上面这种解题方法叫做拆项法，按此方法计算： $(- 4 \frac{7}{8}) + (+ 8 \frac{1}{4}) + (- 3 \frac{1}{8})$

查看试题解析
17. 图1中，有一个平行四边形；
图2中，由2个相同的平行四边形拼成一排的图形，这图形中可以找到3个平行四边形；
图3中，由3个相同的平行四边形拼成一排的图形，这图形中可以找到6个平行四边形；
由此我们可以提出一个这样的问题：
图4中，由4个相同的平行四边形拼成一排的图形中，可以找到几个平行四边形？
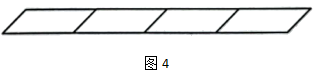
答：10个
请你根据以上事实，将一些相同的平行四边形横向或纵向拼接，由此提出一个数学问题，并写出答案．

查看试题解析
18. 3²－1²＝8×1
5²－3²＝8×2

7²－5²＝8×3

9²－7²＝8×4

……

观察上面的一系列等式，你能发现什么规律？用代数式表示这个规律，并用这个规律计算2001²－1999²的值.

查看试题解析
19. 已知下列等式：①2²﹣1²=3；②3²﹣2²=5；③4²﹣3²=7，…

(1)、请仔细观察前三个等式的规律，写出第⑥个等式；

(2)、请你找出规律，写出第n个等式（用含n的式子表示）；

(3)、利用（2）中发现的规律计算：1+3+5+…+199．

查看试题解析
20. 观察下列各等式：
1－3＝－2；
1－3＋5－7＝(－2)＋(－2)＝－4；
1－3＋5－7＋9－11＝(－2)＋(－2)＋(－2)＝－6；
…
根据以上各等式的规律，计算：
1－3＋5－7＋…＋2017－2019.

查看试题解析
21. 观察下列等式： $\frac{1}{1 \times 2}$ =1﹣ $\frac{1}{2}$ ， $\frac{1}{2 \times 3}$ = $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ， $\frac{1}{3 \times 4}$ = $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ，…．
将以上三个等式两边分别相加得： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ =1﹣ $\frac{1}{2}$ + $\frac{1}{2}$ ﹣ $\frac{1}{3}$ + $\frac{1}{3}$ ﹣ $\frac{1}{4}$ =1﹣ $\frac{1}{4}$ = $\frac{3}{4}$ ．

(1)、猜想并写出： $\frac{1}{n (n + 1)}$ = ．

(2)、直接写出下列各式的计算结果：
① $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{2016 \times 2017}$ =；

② $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{n (n + 1)}$ = ．

(3)、探究并计算： $\frac{1}{2 \times 4}$ + $\frac{1}{4 \times 6}$ + $\frac{1}{6 \times 8}$ +…+ $\frac{1}{2014 \times 2016}$ ．

查看试题解析
22. 观察下列单项式：﹣x，3x² ， ﹣5x³ ， 7x⁴ ， …﹣37x¹⁹ ， 39x²⁰的特点，写出第n个单项式．为了解决这个问题，特提供下面的解题思路：

(1)、先观察这组单项式系数的符号及绝对值的规律；

(2)、再看这组单项式次数的规律．请根据你的经验，猜想第n个单项式可表示为．（用含n的式子表示）

查看试题解析
23. 你能化简（a﹣1）（a⁹⁹+a⁹⁸+a⁹⁷+…+a²+a+1）吗？我们不妨先从简单情况入手，发现规律，归纳结论．

(1)、先填空：（a﹣1）（a+1）=；（a﹣1）（a²+a+1）=；
（a﹣1）（a³+a²+a+1）=；…
由此猜想（a﹣1）（a⁹⁹+a⁹⁸+a⁹⁷+…+a²+a+1）= ．

(2)、利用这个结论，你能解决下面两个问题吗？
①2¹⁹⁹+2¹⁹⁸+2¹⁹⁷+…+2²+2+1；
②若a⁵+a⁴+a³+a²+a+1=0，则a⁶等于多少？

查看试题解析

（北师大版）2022-2023学年度第一学期七年级数学 探索与表达规律 期中复习

一、单选题

二、填空题

三、解答题

（北师大版）2022-2023学年度第一学期七年级数学探索与表达规律期中复习