苏科版数学2022-2023学年九年级上册一元二次方程单元测试卷

试卷更新日期：2022-10-19 类型：单元试卷

进入出卷网下载

一、单选题（每题4分，共40分）

1. 将一元二次方程 $3 x^{2} - 1 = 5 x$ 化为一般形式后，其中二次项系数、一次项系数、常数项分别是（）

A、3，5，-1 B、-3，5，1 C、3，-5，-1 D、3，-5，13

查看试题解析
2. 若关于x的一元二次方程 $k x^{2} - 4 x + 1 = 0$ 有两个不相等实根，则k的取值范围是（　　　）

A、 $k < 4$ B、 $k > - 4$ C、 $k < 4$ 且 $k \neq 0$ D、 $k > - 4$ 且 $k \neq 0$

查看试题解析
3. 某机械厂七月份生产零件100万个，第三季度生产零件392万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是（）

A、100（1+x）²＝392 B、100+100（1+x）²＝392 C、100+100（1+x）+100（1+2x）＝392 D、100+100（1+x）+100（1+x）²＝392

查看试题解析
4. 已知等腰△ABC的两边分别是方程x²-10x+21=0的两个根，则△ABC的周长为（）

A、17 B、13 C、11 D、13或17

查看试题解析
5. 在一次篮球邀请赛中，参赛的每两个队之间都要赛一场，共赛45场，设共有x个队参赛、根据题意可列方程为（）

A、 $\frac{x (x - 1)}{2} = 45$ B、x（x﹣1）＝45 C、 $\frac{x (x + 1)}{2} = 45$ D、x（x+1）＝45

查看试题解析
6. 设 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - 5 x - 4 = 0$ 的两个实数根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值是（）

A、 $- \frac{5}{4}$ B、 $\frac{5}{4}$ C、 $\frac{\sqrt{41}}{4}$ D、 $- \frac{\sqrt{41}}{4}$

查看试题解析
7. 如表是代数式ax²+bx的值的情况，根据表格中的数据，可知方程ax²+bx=6的根是（）
x
……
-3
-2
-1
0
1
2
3
4
……
ax²+bx
……
12
6
2
0
0
2
6
12
……

A、x₁=0，x₂=1 B、x₁=-1，x₂=2 C、x₁=-2，x₂=3 D、x₁=-3，x₂=4

查看试题解析
8. 如图，将图1的正方形剪成四块，恰能拼成图2的矩形，则 $\frac{b}{a} =$ （）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 3}{2}$ C、 $\frac{\sqrt{5} + 1}{2}$ D、 $\sqrt{2} + 1$

查看试题解析
9. 如图，在△ABC中，AB＝AC＝6，∠BAC＝120°，过点A作AD⊥BA交BC于点D，过点D作DE⊥BC交AC于点E，则AE的长为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图，在活动课上，老师画出边长为2的正方形ABCD ，让同学们按以下步骤完成画图：
⑴画出AD的中点E ，连接BE；

⑵以点E为圆心，EB长为半径画弧，交DA的延长线于点F；

⑶以AF为边画正方形AFGH ，点H在AB边上．在画出的图中有一条线段的长是方程x²+2x﹣4＝0的一个根．这条线段是（）

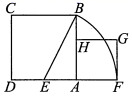A、线段BH B、线段BE C、线段AE D、线段AH

查看试题解析

二、填空题（每题5分，共25分）

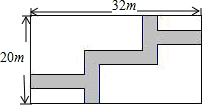
11. 已知x²－6x+8＝0的两个根分别是等腰三角形的底和腰，则这个三角形的面积是．

查看试题解析
12. 如图，在宽为20m，长为32m的矩形地面上修筑同样宽的道路，余下的部分种上草坪，要使草坪的面积为540m² ，求道路的宽若设道路宽为xm，则根据题意可列方程为

查看试题解析
13. “新冠肺炎”防治取得战略性成果，若有一个人患了“新冠肺炎”，经过两轮传染后共有25个人患了“新冠肺炎”，则每轮传染中平均一个人传染了人．

查看试题解析
14. 有一张矩形纸板，长为80cm，宽为60cm，在它的四角各减去一个相同的小正方形；然后折叠成一个无盖的长方形纸盒．若纸盒的底面积（图中阴影部分）为 $1500 c m^{2}$ ，剪去的小正方形的边长为．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $A C = 50 m$ ， $C B = 40 m$ ， $∠ C = 90 °$ ，点 $P$ 从点 $A$ 开始沿 $A C$ 边向点C以 $2 m / s$ 的速度移动，同时另一个点 $Q$ 从点C开始沿 $C B$ 以 $3 m / s$ 的速度移动，当△PCQ的面积等于450m²时，经过的时间是.

查看试题解析

三、综合题（共7题，共85分）

16. 用适当的方法解下列一元二次方程：

(1)、 $x^{2} - 4 x - 6 = 0$ （用配方法解）

(2)、 $\frac{1}{2} x^{2} - \sqrt{2} x + 1 = 0$

(3)、 $3 x (x + 2) = 5 (x + 2)$

(4)、 $16 (3 x - 2)^{2} = (x + 5)^{2}$

查看试题解析
17. 某花卉生产基地举行花卉展览，如图所示是用这两种花卉摆成的图案，白色圆点为盆景，灰色圆点为盆花．图1中盆景数量为2，盆花数量为2；图2中盆景数量为4，盆花数量为6；图3中盆景数量为6，盆花数量为12……
按照以上规律，解决下列问题：

(1)、图6中盆景数量为，盆花数量为；

(2)、已知该生产基地展出以上两种花卉在某种图案中的数量之和为130盆，分别求出该图案中盆景和盆花的数量；

(3)、若有n（n为偶数，且 $n \geq 2$ ）盆盆景需要展出（只摆一种图案），照此组合图案，需要盆花的数量为．（用含n的代数式表示）

查看试题解析
18. 如图，在足够大的空地上有一段长为a米的旧墙，农场决定利用旧墙和篱笆围成中间隔有一道篱笆的矩形菜园ABCD，其中AD≤a，已知矩形菜园的一边靠墙，共用了60米篱笆．

(1)、若a＝20，所围成的矩形菜园的面积为225平方米，求所利用旧墙AD的长；

(2)、求矩形菜园ABCD面积的最大值．

查看试题解析
19. 关于x的一元二次方程x²﹣3x+k＝0有实数根．

(1)、求k的取值范围；

(2)、如果k是符合条件的最大整数，且一元二次方程（m﹣1）x²+x+m﹣3＝0与方程x²﹣3x+k＝0有一个相同的根，求此时m的值．

查看试题解析
20. “阳光玫瑰”葡萄品种是广受各地消费者的青睐的优质新品种，在我国西部区域广泛种植，某葡萄种植基地2018年种植“阳光玫瑰”100亩，到2020年“阳光玫瑰”的种植面积达到256亩.

(1)、求该基地这两年“阳光攻瑰”种植面积的平均年增长率，

(2)、市场调查发现，当“阳光玫瑰”的售价为20元/千克时，每天能售出200千克，售价每降价1元，每天可多售出45千克.
①若降价x（0≤x≤20）元，每天能售出多少千克？（用x的代数式表示）

②为了推广宣传，基地决定降价促销，同时尽量减少库存，已知该基地“阳光玫瑰”的平均成本价为10元/千克，若要销售“阳光玫瑰”每天获利2125元，则售价应降低多少元？

查看试题解析
21. 如图，四边形ACDE是证明勾股定理时用到的一个图形，a，b，c是Rt△ABC和Rt△BED边长，易知AE＝ $\sqrt{2}$ c，这时我们把关于x的形如ax²+ $\sqrt{2}$ cx+b＝0的一元二次方程称为“勾系一元二次方程”．
请解决下列问题：

(1)、试判断方程 $x^{2} + 2 x + 1 = 0$ 是否为 “勾系一元二次方程”；

(2)、求证：关于x的“勾系一元二次方程”ax²+ $\sqrt{2}$ cx+b＝0必有实数根；

(3)、若x＝﹣1是“勾系一元二次方程”ax²+ $\sqrt{2}$ cx+b＝0的一个根，且四边形ACDE的周长是12，求△ABC面积．

查看试题解析
22. 我们知道： $x^{2} - 6 x = (x^{2} - 6 x + 9) - 9 = (x - 3)^{2} - 9$ ； $- x^{2} + 10 = - (x^{2} - 10 x + 25) + 25 = - (x - 5)^{2} + 25$ ，这一种方法称为配方法，利用配方法请解以下各题：

(1)、按上面材料提示的方法填空： $a^{2} - 4 a =$ $=$ $. - a^{2} + 12 a =$ $=$ ．

(2)、探究：当 $a$ 取不同的实数时在得到的代数式 $a^{2} - 4 a$ 的值中是否存在最小值？请说明理由．

(3)、应用：如图．已知线段 $A B = 6$ ， $M$ 是 $A B$ 上的一个动点，设 $A M = x$ ，以 $A M$ 为一边作正方形 $A M N D$ ，再以 $M B$ 、 $M N$ 为一组邻边作长方形 $M B C N .$ 问：当点 $M$ 在 $A B$ 上运动时，长方形 $M B C N$ 的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．

查看试题解析

x	……	-3	-2	-1	0	1	2	3	4	……
ax²+bx	……	12	6	2	0	0	2	6	12	……

苏科版数学2022-2023学年九年级上册一元二次方程 单元测试卷

一、单选题（每题4分，共40分）

二、填空题（每题5分，共25分）

三、综合题（共7题，共85分）

苏科版数学2022-2023学年九年级上册一元二次方程单元测试卷