广西百色市2021-2022学年高一上学期数学期末调研测试试卷
试卷更新日期:2022-10-18 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 命题:“ ”的否定是( )A、 B、 C、 D、3. 设 , , , 则( )A、 B、 C、 D、4. ( )A、 B、 C、 D、5. 函数的定义域为( )A、 B、 C、 D、6. 已知幂函数在上单调递减,则m的值为( )A、0 B、1 C、0或1 D、7. 函数的图象的一个对称中心是( )A、 B、 C、 D、8. 已知函数 为 上偶函数,且 在 上的单调递增,若 ,则满足 的 的取值范围是( )A、 B、 C、 D、
二、多选题
-
9. 若 ,则下列不等式正确的是( )A、 B、 C、 D、10. 不等式成立的一个充分不必要条件是( )A、 B、或 C、 D、或11. 若函数(且)的图象如图所示,则下列函数图象不正确的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 12. 已知函数 , ,则下列结论正确的是( )A、函数 的图象关于点 对称 B、函数 的最小正周期是 C、函数 在区间 上单调递减 D、把函数 图象上所有的点向右平移 个单位长度得到的函数图象的对称轴与函数 图象的对称轴完全相同
12. 已知函数 , ,则下列结论正确的是( )A、函数 的图象关于点 对称 B、函数 的最小正周期是 C、函数 在区间 上单调递减 D、把函数 图象上所有的点向右平移 个单位长度得到的函数图象的对称轴与函数 图象的对称轴完全相同三、填空题
-
13. 设函数 , 则.14. 如图,扇形的面积是1,它的弧长是2,则扇形的圆心角的弧度数为 .
 15. 若 , , , 则的最小值为.16. 已知函数 ,其所有的零点依次记为 ,则 .
15. 若 , , , 则的最小值为.16. 已知函数 ,其所有的零点依次记为 ,则 .四、解答题
-
17. 已知集合 , .(1)、若 , 求 , ;(2)、若 , 求实数的取值范围.18. 计算下列各式的值:(1)、;(2)、.19. 已知 , 求下列各式的值.(1)、;(2)、.20. 已知函数f(x)=Asin(ωx+φ)的图象的一部分如图所示.
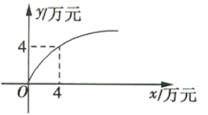
 (1)、求函数f(x)的解析式;(2)、当时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x值.21. 某企业生产 , 两种产品,根据市场调查与预测,产品的利润与投资成正比,其关系如图(1)所示;产品的利润与投资的算术平方根成正比,其关系如图(2)所示(注:利润和投资的单位均为万元).
(1)、求函数f(x)的解析式;(2)、当时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x值.21. 某企业生产 , 两种产品,根据市场调查与预测,产品的利润与投资成正比,其关系如图(1)所示;产品的利润与投资的算术平方根成正比,其关系如图(2)所示(注:利润和投资的单位均为万元).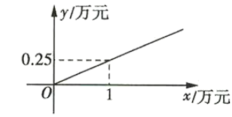
图(1) 图(2)
(1)、分别求 , 两种产品的利润关于投资的函数解析式.(2)、已知该企业已筹集到18万元资金,并将全部投入 , 两种产品的生产.①若平均投入两种产品的生产,可获得多少利润?
②如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润为多少万元?
22. 已知函数.(1)、证明为奇函数;(2)、若在上为单调函数,当时,关于的方程:在区间上有唯一实数解,求的取值范围.