广东省汕尾市2021-2022学年高一上学期数学期末考试试卷
试卷更新日期:2022-10-18 类型:期末考试
一、单选题
-
1. 若集合 , ,则 ( )A、{3} B、{5} C、 D、2. 若 , 为第四象限角,则的值为( )A、 B、 C、 D、3. 函数的零点所在区间为( )A、 B、 C、 D、4. 函数的定义域是( )A、 B、 C、 D、5. 当时,在同一平面直角坐标系中,与的图象是( )A、
 B、
B、 C、
C、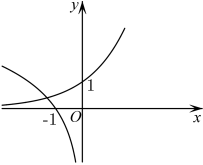 D、
D、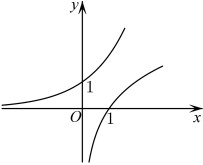 6. 已知角的顶点与平面直角坐标系的原点重合,始边与x轴的正半轴重合,终边经过点 , 若 , 则的值为( ).A、 B、 C、 D、7. 若 , , , 则( )A、 B、 C、 D、8. 酒驾是严重危害交通安全的违法行为.根据国家有关规定:驾驶人血液中的酒精含量大于(或等于)毫克/毫升,小于毫克/毫升的情况下驾驶机动车属于饮酒驾车;含量大于(或等于)毫克/毫升的情况下驾驶机动车属于醉酒驾车.假设某驾驶员一天晚上点钟喝了一定量的酒后,其血液中酒精含量上升到毫克/毫升.如果在停止喝酒后,他血液中酒精含量以每小时的速度减少,则他次日上午最早( )点(结果取整数)开车才不构成酒驾.(参考数据: , )A、 B、 C、 D、
6. 已知角的顶点与平面直角坐标系的原点重合,始边与x轴的正半轴重合,终边经过点 , 若 , 则的值为( ).A、 B、 C、 D、7. 若 , , , 则( )A、 B、 C、 D、8. 酒驾是严重危害交通安全的违法行为.根据国家有关规定:驾驶人血液中的酒精含量大于(或等于)毫克/毫升,小于毫克/毫升的情况下驾驶机动车属于饮酒驾车;含量大于(或等于)毫克/毫升的情况下驾驶机动车属于醉酒驾车.假设某驾驶员一天晚上点钟喝了一定量的酒后,其血液中酒精含量上升到毫克/毫升.如果在停止喝酒后,他血液中酒精含量以每小时的速度减少,则他次日上午最早( )点(结果取整数)开车才不构成酒驾.(参考数据: , )A、 B、 C、 D、二、多选题
-
9. 下列函数中,以为最小正周期,且在上单调递减的为( )A、 B、 C、 D、10. 下列说法正确的是( )A、“”是“”的充分不必要条件 B、“”是“”的必要不充分条件 C、“对任意一个无理数 , 也是无理数”是真命题 D、命题“ , ”的否定是“ , ”11. 设 , , 若 , 则实数的值可以为( )A、2 B、 C、 D、012. 已知 , 则下列结论正确的是( )A、 B、函数单调递增区间为 C、当时,方程有三个不等实根 D、当且仅当时,方程有两个不等实根
三、填空题
-
13. 全集 , 集合 , 则 .14. 若扇形的面积为9,圆心角为2弧度,则该扇形的弧长为 .15. 函数为奇函数,且对任意互不相等的 , , 都有成立,且 , 则的解集为 .16. 若存在常数k和b,使得函数和对其公共定义域上的任意实数x都满足:和恒成立(或和恒成立),则称此直线为和的“隔离直线”.已知函数 , , 若函数和之间存在隔离直线 , 则实数b的取值范围是 .
四、解答题
-
17.(1)、求值:;(2)、已知 , 化简求值: .18. 已知函数 , .(1)、求的最小正周期;(2)、求的单调递增区间;(3)、当时,求的最大值和最小值.19. 已知函数( , 为常数,且)的图象经过点 , .(1)、求函数的解析式;(2)、若关于不等式对都成立,求实数的取值范围.20. 在①;②关于x的不等式的解集是这两个条件中任选一个,补充在下面的问题(1)中并解答,若同时选择两个条件作答,以第一个作答计分.(1)、已知_________,求关于的不等式的解集;(2)、在(1)的条件下,若非空集合 , , 求实数的取值范围.21. 某城市2021年12月8日的空气质量指数(Air Quality Inex,简称AQI)与时间(单位:小时)的关系满足下图连续曲线,并测得当天AQI的最大值为103.当时,曲线是二次函数图象的一部分;当时,曲线是函数(且)图象的一部分,根据规定,空气质量指数AQI的值大于或等于100时,空气就属于污染状态.
 (1)、求函数的解析式;(2)、该城市2021年12月8日这一天哪个时间段的空气属于污染状态?并说明理由.22. 已知函数 .(1)、根据函数单调性的定义,证明在区间上单调递减,在区间上单调递增;(2)、令 , 若对 , , 都有成立,求实数的取值范围.
(1)、求函数的解析式;(2)、该城市2021年12月8日这一天哪个时间段的空气属于污染状态?并说明理由.22. 已知函数 .(1)、根据函数单调性的定义,证明在区间上单调递减,在区间上单调递增;(2)、令 , 若对 , , 都有成立,求实数的取值范围.