甘肃省张掖市2021-2022学年高一上学期数学期末考试试卷
试卷更新日期:2022-10-18 类型:期末考试
一、单选题
-
1. 已知 , 则为( )A、 B、2 C、3 D、-1或32. 若 , , 则下列结论正确的是( )A、 B、 C、 D、a,b大小不确定3. 已知幂函数在上单调递减,则( )A、 B、5 C、 D、14. 下列函数中,既是奇函数又在定义域上是增函数的是( )A、 B、 C、 D、5. 函数的单调递减区间是( )A、() B、() C、() D、()6. 函数的图象大致是( )A、
 B、
B、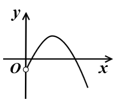 C、
C、 D、
D、 7. 设 , , , 则 , , 的大小关系( )A、 B、 C、 D、8. 为了给地球减负,提高资源利用率,2020年全国掀起了垃圾分类的热潮,垃圾分类已经成为新时尚.假设某市2020年全年用于垃圾分类的资金为3000万元,在此基础上,以后每年投入的资金比上一年增长20%,则该市全年用于垃圾分类的资金开始超过1亿元的年份是(参考数据: , , )( )A、2026年 B、2027年 C、2028年 D、2029年
7. 设 , , , 则 , , 的大小关系( )A、 B、 C、 D、8. 为了给地球减负,提高资源利用率,2020年全国掀起了垃圾分类的热潮,垃圾分类已经成为新时尚.假设某市2020年全年用于垃圾分类的资金为3000万元,在此基础上,以后每年投入的资金比上一年增长20%,则该市全年用于垃圾分类的资金开始超过1亿元的年份是(参考数据: , , )( )A、2026年 B、2027年 C、2028年 D、2029年二、多选题
-
9. 下列关系式错误的是( )A、 B、 C、 D、10. 下列说法正确的是( )A、手表时针走过小时,时针转过的角度为 B、把化为弧度是 C、命题“若角的终边经过点 , 则 ”为真命题 D、已知角为第二象限角,且 , 则11. 若函数只有一个零点3,那么函数的零点是( ).A、 B、 C、 D、12. 已知定义在上的奇函数满足. 当时, , 则下列结论正确的是( )A、的图象关于轴对称 B、 C、 D、
三、填空题
-
13. 命题“ , ”的否定为.14. 已知圆心角为的扇形的面积为 , 则该扇形的半径为.15. 函数定义域为.16. 若不等式在上恒成立,则实数a的取值范围为.
四、解答题
-
17. 已知全集 , 集合 , 集合.(1)、若 , 求;(2)、若“”是“”必要不充分条件,求实数的取值范围.18. 化简计算:(1)、计算:;(2)、化简: .19. 已知函数.(1)、请用“五点法”画出函数在上的图象(先列表,再画图);(2)、求在上的值域;(3)、求使取得最值时的取值集合,并求出最值.20. 设函数 .(1)、若不等式的解集是 , 求不等式的解集;(2)、当时,在上恒成立,求实数的取值范围.