广西防城港市上思县2022-2023学年八年级上学期学习成果监测(一)数学试题
试卷更新日期:2022-10-18 类型:月考试卷
一、选择题(本大题12小题,每小题3分,共36分)
-
1. 下列长度的三条线段能首尾相接构成三角形的是( )A、 , , B、 , , C、 , , D、 , ,2. 已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( )A、11 B、5 C、2 D、13. 下列图形中具有稳定性的是( )A、平行四边形 B、三角形 C、长方形 D、正方形4. 如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC 的( )
 A、中线 B、中位线 C、高线 D、角平分线5. 一个正多边形每个内角与它相邻外角的度数比为3∶1,则这个正多边形是( )A、正方形 B、正六边形 C、正八边形 D、正十边形6. 如图,已知 , 于点 , 若 , 则的度数是( )
A、中线 B、中位线 C、高线 D、角平分线5. 一个正多边形每个内角与它相邻外角的度数比为3∶1,则这个正多边形是( )A、正方形 B、正六边形 C、正八边形 D、正十边形6. 如图,已知 , 于点 , 若 , 则的度数是( ) A、30° B、40° C、50° D、60°7. 具备下列条件的△ABC中,不是直角三角形的是( )A、∠A=∠B=3∠C B、∠A﹣∠B=∠C C、∠A +∠B=∠C D、∠A∶∠B∶∠C=1∶2∶38. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
A、30° B、40° C、50° D、60°7. 具备下列条件的△ABC中,不是直角三角形的是( )A、∠A=∠B=3∠C B、∠A﹣∠B=∠C C、∠A +∠B=∠C D、∠A∶∠B∶∠C=1∶2∶38. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )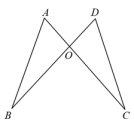 A、SSS B、SAS C、AAS D、HL9. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A、SSS B、SAS C、AAS D、HL9. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( ) A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED10. 如图,在△ABC中, , D是上一点,于点E, , 连接 , 若 , 则等于( )
A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED10. 如图,在△ABC中, , D是上一点,于点E, , 连接 , 若 , 则等于( ) A、6 B、7 C、8 D、911. 如图,AD是的角平分线, , 若 , 则的面积为( )
A、6 B、7 C、8 D、911. 如图,AD是的角平分线, , 若 , 则的面积为( )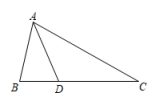 A、3 B、2 C、 D、112. 如图所示,在中, , AD平分 , 于点E,则下列结论:① DA平分;②∠=∠;③DE平分∠;④ . 其中
A、3 B、2 C、 D、112. 如图所示,在中, , AD平分 , 于点E,则下列结论:① DA平分;②∠=∠;③DE平分∠;④ . 其中正确的有
 A、①② B、①④ C、③④ D、①②④
A、①② B、①④ C、③④ D、①②④二、填空题(本大题共6题,每题3分,共18分)
-
13. 正八边形的一个内角的度数是 度。
14. 一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是.15. 如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB=°. 16. 如图,在中,、分别是、上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是.
16. 如图,在中,、分别是、上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是. 17. 在△ABC中,AC=5 cm,AD是△ABC的中线,把△ABC的周长分为两部分,若其差为3 cm,则BA= .18. 如图所示,中, . 直线l经过点A,过点B作BE⊥l于点E,过点C作CF⊥l于点F.若BE=2,CF=5,则EF= .
17. 在△ABC中,AC=5 cm,AD是△ABC的中线,把△ABC的周长分为两部分,若其差为3 cm,则BA= .18. 如图所示,中, . 直线l经过点A,过点B作BE⊥l于点E,过点C作CF⊥l于点F.若BE=2,CF=5,则EF= .
三、解答题(本大题共8小题,共66分.)
-
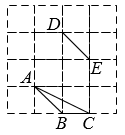
19. 如图,在4×4的正方形网格中,A,B,C,D,E是网格线交点.请画出一个△DEF,使得△DEF与△ABC全等
 20. 已知:如图,E、F是AB上两点,AC∥BD,AC=BD,AE=BF,问:CF=DE吗?说明理由.
20. 已知:如图,E、F是AB上两点,AC∥BD,AC=BD,AE=BF,问:CF=DE吗?说明理由. 21. 如图,在△ABC中,CD为∠ACB的角平分线,DE∥BC,∠A=65°,∠B=35°,求∠EDC的度数.
21. 如图,在△ABC中,CD为∠ACB的角平分线,DE∥BC,∠A=65°,∠B=35°,求∠EDC的度数. 22. 如图所示,在△ABC中,AE是角平分线,AD是高,∠BAC=80°,∠EAD=10°,求∠B的度数
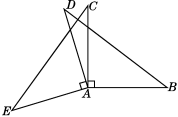
22. 如图所示,在△ABC中,AE是角平分线,AD是高,∠BAC=80°,∠EAD=10°,求∠B的度数 23. 如图,AD⊥AE,AB⊥AC, AD=AE,AB=AC.求证:△ABD≌△ACE.
23. 如图,AD⊥AE,AB⊥AC, AD=AE,AB=AC.求证:△ABD≌△ACE.